วันแรก

ข้อ 7.
โดยอุปนัยทางคณิตศาสตร์จะพิสูจน์ได้ว่า
f(2n) = 2n และ f(2n+1) = 1 เมื่อ n >= 1

ข้อ 8.
f(x + f(y)) = 2x + 4y + 2547
f(0) = -2f(y) + 4y + 2547
f(y) = (4y + 2547 - f(0)) / 2
x + f(y) = x + (4y + 2547 - f(0)) / 2
f(x + f(y)) = f(x + (4y + 2547 - f(0)) / 2)
2x + 4y + 2547 = (4[x + (4y + 2547 - f(0)) / 2] + 2547 - f(0)) / 2
4x + 8y + 2(2547) = 4[x + (4y + 2547 - f(0)) / 2] + 2547 - f(0)
4x + 8y + 2(2547) = 4x + 8y + 3(2547) - 3 f(0)
f(0) = 2547 / 3

บอกได้คำเดียวว่า "ยากส์" :mad:

คำตอบข้อ 8. (วันแรก) ของคุณ <คิดด้วยคน> ถ้าให้ y = 0 ในบรรทัดที่ 2 ก็จะหา f(0) ได้ทันทีเลยครับ

คราวนี้น่าจะถูกแล้ว. ข้อ 3 วันที่สอง ถ้าให้ S(m, n) แทนจำนวนวิธีในการจัด โดยที่ m = จำนวนคน, n = จำนวนครั้งของการสลับ จะได้ว่า S(18, 150) = S(18, 3) = 951 . No comment :eek: ใครคิดออกช่วยลองตรวจดูว่าคำตอบตรงกันหรือเปล่า

ส่วนข้ออื่น ๆ ที่ผมลองแตะไป ให้คำตอบเพิ่มเติมจากคุณคิดด้วยคน มี
วันแรก : ข้อ 1)5ึ6/18 ข้อ 15) 2002 ข้อ 16) กำลัง attack อยู่ ข้อ 17) 4 ส่วน 2 ข้อท้ายสุด อันนี้ใช้ความจำ เพราะปากระดาษทดทิ้งไปแล้ว คือ ข้อ 20) ab/(a + b) ข้อ 21) 5

วันที่สอง : ข้อ 1 ,จำได้ว่า attack ไปแล้วแต่รู้สึกยังติดสมการที่โดยหลักการ sol ได้ แต่ยัง sol ไม่ออก . ข้อ 4. ได้แล้วใช้ตรีโกณตอนเริ่มต้น เพื่อหาสูตรของพื้นที่สี่เหลี่ยมใด ๆ ก่อนนั่นเอง แล้วค่อยโยงไปอสมการของโจทย์ ถ้าจำไม่ผิดรู้สึกว่าอสมการของโจทย์ยังไม่แหลมพอ ข้อที่เหลือจะค่อย ๆ ลองพยายาม sol สักวันละข้อสองข้อ.

ว่าแต่คุณอ้วนกับคุณ warut ยังไม่ลอง attack บ้างหรือครับ. น้อง ๆ ที่กำลังจะสอบโอลิมปิกของ สสวท. ทั้งหลายด้วย ไม่ลอง attack ดูบ้าง ?

จะพยายามครับผม :D

สำหรับคราวนี้ขอประเดิมด้วยข้อ 2 ของวันแรกก่อนเพราะผมคิดว่าข้อนี้มีปัญหาครับ
ข้อนี้ตามความคิดของผมคิดว่าคำตอบคือ "หาค่าไม่ได้" ซึ่งเดาว่าคงไม่ใช่คำตอบที่ผู้
ตั้งโจทย์ต้องการให้ตอบกระมัง

พิสูจน์
เห็นได้ชัดว่าจำนวนจริง a และ b ต่างก็ไม่เท่ากับศูนย์
จาก a⁶ - 3a²b⁴ = 3 จะได้ a⁴ - 3b⁴ = 3/a²
จาก b⁶ - 3a⁴b² = 3ึ2 จะได้ b⁴ - 3a⁴ = 3ึ2/b²
จับสองสมการบวกกันจะได้ -2a⁴ - 2b⁴ = 3/a² + 3ึ2/b²
จะเห็นว่าข้างซ้ายของสมการเป็นลบแต่ข้างขวาเป็นบวก จึงเกิดข้อขัดแย้งขึ้น

ผู้ออกโจทย์คงไม่ได้ระวังว่าไม่มีคำตอบที่ทั้ง a และ b เป็นจำนวนจริง (ปัญหาทำนองนี้
เคยเกิดขึ้นเมื่อปีที่แล้วด้วย) คุณ gon (และอีกหลายคน) อาจจะคิดว่าผมคิดมากอีก
("เราก็ไม่ต้องสนสิว่า a กับ b จะเป็นจำนวนจริงหรือจำนวนเชิงซ้อน เราแค่หาค่าของ
a⁴ + b⁴ ออกมาก็พอ") แต่ผมขอให้ข้อมูลเพิ่มเติมอีกนิดว่าถ้าเรายอมให้ a และ b เป็น
จำนวนเชิงซ้อนแล้วค่าของ a⁴ + b⁴ จะมีได้มากกว่าหนึ่งค่าครับ!

ข้อ 20 (คิดออกข้อนี้ข้อเดียว - -'')
เมื่อวาดรูปก็จะได้รูปดังที่แนบมาด้วย
พบว่า
D ABD ~ D EFD ---> x/a = FD/BD -----(1)
D BCD ~ D BEF ---> x/b = BF/BD -----(2)
(1)+(2) : x(1/a +1/b) = (BF+FD)/BD
x[(a+b)/ab] = BD/BD = 1
x = ab/(a+b) #

ข้อ 8 วันแรก

เนื่องจาก f:RฎR ดังนั้น แทน x = -f(0) และแทน y = 0
ได้ว่า f(-f(0) + f(0)) = 2(-f(0)) + 4(0) + 2547
f(0) = -2f(0) +2547
f(0) = 2547/3
_________________________________________________

ข้อ 2 วันที่ 2

กำหนด f(x + y) = f(x) + f(y) + 2547 -----------------(*)
และ f(2004) = 2547

จะพิสูจน์ว่า f(nx) = nf(x) + (n-1)2547 , เมื่อ n เป็นจำนวนเต็มบวก
เนื่องจาก f(1(x)) = 1f(x) + (1-1)2547 = f(1)
สมมติให้ f(kx) = kf(x) + (k-1)2547 -----------------(**)
จาก(*) f(kx+x) = f(kx) + f(x) +2547
จาก(**) f((k+1)x) = kf(x) + (k-1)2547 + f(x) + 2547 = (k+1)f(x) + ((k+1)-1)2547
ดังนั้น f(nx) = nf(x) + (n-1)2547 , เมื่อ n เป็นจำนวนเต็มบวก

ได้ว่า f(2547ท2004) = 2547f(2004) + 2546ท2547 ----(1)
และ f(2004ท2547) = 2004f(2547) + 2003ท2547 ----(2)
(1)=(2)
2547f(2004) + 2546ท2547 = 2004f(2547) + 2003ท2547
2547(2547) + 2546ท2547 = 2004f(2547) + 2003ท2547
ได้ว่า f(2547) = 2547ท1545/1002

ข้อ 19. ผมทำแบบ basic ไม่ออกสักที เหนื่อยใจเลยต้องใช้วิชาแคลคูลัส คือ Lagrange Multiplier (ลากรอง มัลติพลายเออร์) solve เลย ราบรื่นฉลุย ลองดูนะครับ. (ใครทำแบบง่าย ๆ ได้ ก็ดี)

โดย Lagrange Multiplier : ให้ f(a, b, c) = a + 2b + 3c \ grad f(a, b, c) = (1, 2, 3) และ g(a, b, c) = 9a² + 4b² + c² \ grad g(a, b, c) = (18a, 8b, 2c)
จะมี l ซึ่ง grad f(a, b, c) = l grad g(a, b, c) ด้วยเงื่อนไข 9a² + 4b² + c² = 91
จะได้ a = 1/3 \ (a, b, c) = (1/3,3/2, 9)

ส่วนข้อ 18. ก็ลอง กรองดูแล้ว แต่รู้สึกถ้าคิดไม่ผิด สมการสุดท้ายของ a จะเป็นสมการกำลังสาม ซึ่งได้คำตอบจำนวนจริงที่ไม่สวย (ถ้าคิดไม่ผิดนะครับ)

อ้อ. ข้อ 2 วันแรก ผมเห็นด้วยกับคุณ warut ครับ. อันที่จริงผมยังไม่ออกหรอกว่าสมการมีปัญหา แต่พอจะ solve ดู โดย sense สมการอีกอัน เครื่องหมายมันควรจะเป็นบวกทั้งหมด เพราะไม่งั้นมันจะ solve ออกมาไม่สวย แต่เมื่อเห็นชัดเช่นนี้ก็น่าจะได้ข้อสรุปว่า โจทย์น่าจะมีปัญหา

เย่...ในที่สุดผมก็อ่านใจผู้ออกโจทย์ข้อ 2 วันแรกออกแล้ว
(a⁴ + b⁴)³ = (a⁶ - 3a²b⁴)² + (b⁶ - 3a⁴b²)² = 3² + (3ึ2)² = 27
ดังนั้น a⁴ + b⁴ = 3 ครับผม :D
โจทย์ข้อนี้จะยุ่งยากน้อยลงถ้าเราให้ A = a² และ B = b² ซะก่อน
จริงๆถ้าโจทย์ให้หา A² + B² โดยที่ A และ B เป็นจำนวนจริง และ
A³ - 3AB² = 3 และ B³ - 3A²B = 3ึ2
ก็จะไม่ทำให้เกิดปัญหาดังกล่าว

เห็นด้วยกับคุณ gon เรื่องข้อ 18 วันแรกครับ คำตอบไม่สวยเอาเสียเลย ซึ่งก็เป็นไปได้
สองอย่างคือคนตั้งโจทย์ใจร้ายมากหรือไม่ก็โจทย์พิมพ์ผิดไปจากที่ตั้งใจไว้

a = (-1 + (53 + 6ึ78)^1/3 + (53 - 6ึ78)^1/3)/6
= 0.657298106138375... เป็นรากจริง (ซึ่งมีอยู่รากเดียว) ของสมการ 2a³ + a² - 1 = 0

b = 4/(a² + 1) = (8 + (8 + 6ึ78)^1/3 + (8 - 6ึ78)^1/3)/3
= 2.793216505472184... ซึ่งก็คือรากจริงรากเดียวของสมการ b³ - 8b² + 26b - 32 = 0

c = 4/(a + 1) = (8 - 2(8 + 6ึ78)^1/3 - 2(8 - 6ึ78)^1/3)/3
= 2.413566989055631... เป็นรากจริงรากเดียวของสมการ c³ - 8c² + 40c - 64 = 0

นั่นคือ abc = 16a/(a + 1)/(a² + 1) = (-8 + 4(307 + 39ึ78)^1/3 + 4(307 - 39ึ78)^1/3)/3
= 4.431250870995745... อันเป็นรากจริงรากเดียวของสมการ p³ + 8p² + 176p - 1024 = 0

Happy Dpromt ครับ. ปัญหาค่อย ๆ ถูกทลายลงเรื่อย ๆ วันนี้มาต่อได้อีกข้อ

ข้อ 16 วันแรก : จงหาสามหลักสุดท้ายของ 2²²⁰⁰⁴ หลังจากไม่ฉลาดอยู่นาน สุดท้ายก็หลุดจนได้ มาดูวิธีที่ไม่ฉลาดกันก่อนครับ.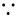

---

2¹⁰ = 1024 บ 24 mod 1000
\ 2²⁰⁰⁴ = 2²⁰⁰⁰ 2⁴ บ24²⁰⁰ 2⁴ mod 1000 บ2⁶⁰⁰ 3²⁰⁰ 2⁴ mod 1000 บ24⁶⁰ 3²⁰⁰2⁴ mod 1000 บ...บ(512)(3²⁸⁵) mod 1000 ... (1)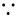
3²⁸⁴ = (10 - 1)¹⁴² โดย ท.บ. ไบโนเมียล จะได้ว่า 3²⁸⁵บ(681)(3) บ43 mod 1000
\ 2²⁰⁰⁴ บ(512)(43) บ43 mod 1000 ฎ จะมีจำนวนเต็มบวก t ซึ่ง 2²⁰⁰⁴ = 16 + 1000t
ในทำนองเดียวกัน จะได้ว่า 2¹⁰⁰⁰ = 376 mod 1000 แต่ 376ⁿ บ376 mod 1000 ทุกจำนวนเต็มบวก n (!!! want to prove. ? !!!)
\ 2²²⁰⁰⁴ = 2^{16 + 1000t} = (2¹⁶)(2¹⁰⁰⁰)^t บ(24)(2⁶)(376)ⁿ บ(536)(376) บ 536 mod 1000
นั่นคือ 3 หลักสุดท้ายของ 2²²⁰⁰⁴ คือ 536

---

Note : หลังจากเริ่มฉลาดขึ้น ก็จะค้นพบ สิ่งต่อไปนี้ เช่น 76ⁿ บ76 mod 1000 เป็นต้น. และ สำหรับข้อนี้ ถ้าใช้ 24^{10n + 2} บ 24² mod 1000 ก็จะเพิ่มความเร็วในการแก้ปัญหาข้อนี้ได้อย่างมากทีเดียว (นี่คือ ข้อสอบที่ให้ทำใน 3 ชั่วโมง แถมยังลึกล้ำขนาดนี้เชียวหรือ ? ผมนั่งคิดข้อนี้เกินกว่า 2 ชั่วโมง เพราะคาดไม่ถึงว่า ถ้าทำตรง ๆ จะ Labour ขนาดนี้ แถมยังซ่อน Trick ไว้ท้ายสุดอีก) ถ้าโจทย์ข้อนี้เปลี่ยนเป็น 7⁷²⁰⁰⁴ ก็จบเกมส์ไปตั้งนานแล้ว ว่างั้นไหมครับ.

ผมก็ไม่ทราบเหมือนกันว่าวิธีไหนเหมาะสมกับข้อ 16 ที่สุด แต่วิธีที่ผมทำน่าจะมีเลขที่
ต้องคิดน้อยกว่าของคุณ gon นะครับ เพียงแต่ต้องทราบ Euler-Fermat Theorem
เท่านั้น (สำหรับคนที่ได้ผ่านเข้ารอบไปฝึกวิชากับเหล่าเทพเจ้า คงจะต้องได้เรียนแน่ครับ)

ทฤษฎีนี้กล่าวว่า ถ้า gcd(a, m) = 1 แล้ว a^f(m) บ 1 (mod m) โดยที่ f คือ Euler's phi function

เริ่มจากพิจารณาใน modulo 125 ก่อนนะครับ เพราะ 1000 = 2³5³ = 8*125
เนื่องจาก f(5³) = 5²f(5) = 25*4 = 100 ดังนั้น 2¹⁰⁰ บ 1 (mod 125)
เราจึงสนใจว่า 2²⁰⁰⁴ บ ? (mod 100)
แต่เรารู้ว่า f(5²) = 5f(5) = 20 ดังนั้น 2²⁰ บ 1 (mod 25)
เพราะฉะนั้น 2²⁰⁰⁴ บ 2⁴ = 16 (mod 25) นั่นคือ 25 | 2²⁰⁰⁴ - 16
แต่เรารู้ว่า 4 | 2²⁰⁰⁴ - 16 ด้วย ดังนั้น 100 | 2²⁰⁰⁴- 16 นั่นคือ 2²⁰⁰⁴ บ 16 (mod 100)
และ 2²⁰⁰⁴ - 3 บ 13 (mod 100) (ทำไมถึงมี -3 เดี๋ยวก็จะเข้าใจครับ)
เพราะฉะนั้น 2^{2^2004 - 3} บ 2¹³ = 8192 บ 67 (mod 125) นั่นคือ 125 | 2^{2^2004 - 3} - 67
ดังนั้น 1000 หาร 8*(2^{2^2004 - 3} - 67) = 2^{2^2004} - 8*67 = 2^{2^2004} - 536 ได้ลงตัว
สรุปเศษของการหารก็คือ 536 ครับ ทำจริงๆน่าจะใช้เวลาน้อยกว่าที่ผมพิมพ์เยอะเลย :D

เหนือชั้นจริง ๆ ครับ. คุณ warut ขอคารวะให้หนึ่งจอก ผมมีดาบแต่ดันใช้ดาบไม่เป็น ตอนนี้กำลัง attack ข้อ 13 อยู่ครับ. เลยขอใช้ Fermat little Theorem ซะเลย ซึ่งจะพิสูจน์ได้ไม่ยากว่า p^{q - 1} + q^{p - 1} บ1 mod pq เมื่อ p, q เป็นจำนวนเฉพาะที่ต่างกัน

---

ปัญหามันอยู่ตรงที่พจน์หลังน่ะครับ. พยายามจะใช้ wilson Theorem แต่ยังไม่ออกเลย กำลังพยายามมอง ๆ อยู่

555...ผมเป็นโรคบ้าจี้ซะด้วยเล่นชมกันอย่างงี้ผมเลยต้องทำต่ออีก... :D

ข้อ 13 เนี่ยตามความเห็นของผมคิดว่าผู้ออกข้อสอบต้องการวัดความรู้ 3 อย่างคือ

1. Fermat's Little Theorem
ถ้า p เป็นจำนวนเฉพาะและ a เป็นจำนวนเต็มที่ p หารไม่ลงตัวแล้ว a^p-1 บ 1 (mod p)
จะเห็นว่าทฤษฎีนี้เป็นกรณีพิเศษของ Euler_Fermat Theorem

2. Wilson's Theorem
p เป็นจำนวนเฉพาะก็ต่อเมื่อ (p - 1)! บ -1 (mod p)

3. Chinese Remainder Theorem
ถ้า gcd(m, n) = 1 แล้วระบบสมการ
x บ r (mod m)
x บ s (mod n)
จะมีคำตอบเพียงหนึ่งเดียวใน modulo mn

ให้ N = 29³⁰ + 31²⁸ + 28!30!
เนื่องจาก 29 | 29³⁰ และ 31²⁸ บ 1 (mod 29) โดย Fermat's Little Theorem และ 29 | 28!30!
ดังนั้น N บ 0 + 1 + 0 = 1 (mod 29)

ต่อไปเราจะหาว่า 28!30! บ ? (mod 31)
โดย Wilson's Theorem เรารู้ว่า 30! บ -1 (mod 31) ----- (*)
นั่นคือ -1 บ 30*29*28! บ (-1)(-2)28! = 2*28! (mod 31)
ดังนั้น 28! บ (-1)((31+1)/2) = -16 (mod 31) ----- (**)
จับ (*) คูณ (**) จะได้ 28!30! บ 16 (mod 31)
แต่เนื่องจาก 29³⁰ บ 1 (mod 31) โดย Fermat 's Little Theorem และ 31 | 31²⁸
ดังนั้น N บ 1 + 0 + 16 = 17 (mod 31)

สรุปว่าเราต้องแก้ระบบสมการ
N บ 1 (mod 29)
N บ 17 (mod 31)

นั่นคือ N = 31s + 17 โดยที่ s เป็นจำนวนเต็ม
ดังนั้น 31s + 17 บ 1 (mod 29)
เพราะฉะนั้น 31s บ 2s บ -16 (mod 29)
สรุปได้ว่า s บ -8 บ 21 (mod 29)
นั่นคือ s = 29t + 21 โดยที่ t เป็นจำนวนเต็ม
ดังนั้น N = 31(29t + 21) + 17 = 31*29t + 31*21 + 17 = 31*29t + 668
สรุปได้ว่าคำตอบที่ต้องการคือ 668 ครับผม :D

วันที่สอง

ข้อ 5.
เห็นได้ชัดว่า 2³ | p² + 2543 เมื่อ p > 2 และ 3 | p² + 2543 เมื่อ p > 3
ดังนั้น 2³* 3 | p² + 2543 เมื่อ p > 3
และ สำหรับ p > 3 จะได้ว่า p² + 2543 ต้องเขียนได้ในรูปของ 2^{3 + x}* 3^{1 + y} เท่านั้น แต่เมื่อพิจารณาค่า x, y ที่ทำให้ได้จำนวนตัวหารบวกที่แตกต่างกันน้อยกว่า 16 ตัวแล้ว พบว่า 2^{3 + x}* 3^{1 + y} < 2543 ทั้งสิ้น นั่นคือ ไม่มี p > 3 ที่เป็นคำตอบที่ต้องการ

สำหรับ p <= 3 พบว่ามีเพียง 2 เท่านั้นที่เป็นคำตอบ

เป็นเว็บที่ดีมากๆๆเลยครับ อยากจะรบกวนด้วยครับ ท่านผู้ใดทราบเว็บคณิตศาสตร์ที่มีโจทย์รัสเซีย กับเยอรมัน ที่เป็นภาษาอังกฤษ แล้วมีโจทย์เด็ดๆมั้งครับ บอกผมด้วยนะครับ ขอบคุณนะครับ และต้องขออภัยด้วยครับที่มาขัดจังหวะ อรรถรสในการแก้โจทย์ ของปิศาจคณิตทั้งหลาย...อิอิอิ