13. กำหนด $$\arctan x-\frac{\pi}{4}=\sum_{k=1}^{2546}\arctan \frac{1}{k^2+k+1}$$ จงหาค่าxที่สอดคล้องกับสมการ

ผมขอเฉลยข้อเก่าละกันครับ

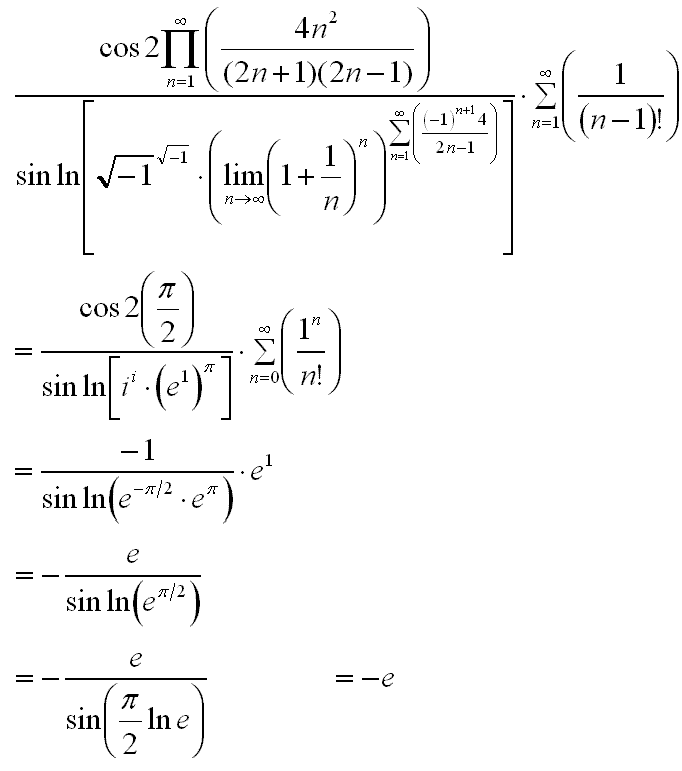ข้อ 13 คุ้นๆนะครับ อ้อ สสวท. ปี '38 รึเปล่า ประมาณปีแถวๆนั้นแหละครับ
จัดรูป $\large \frac{1}{k^2+k+1}=\frac{(k+1)-k}{1+k(k+1)}$
เห็นแล้วคงนึกถึงสูตรของ tan ใช่แล้วครับ จัดรูปหน่อยก็จะได้คำตอบ :D

$$\because \arctan x - \arctan y = \arctan\frac{x-y}{1+xy}$$
$$\therefore \arctan\frac{k+1-k}{1-k(k+1)}=\arctan k+1 - \arctan k$$
$$\sum_{k=1}^{2546} \arctan (k+1) - \arctan k=\arctan2547-\arctan 1$$
$$\arctan x -\frac{\pi}{4} = \arctan2547-\arctan 1$$
$$x=2547$$

14.จงแก้อสมการ
$$\sin x < \cos x$$

ความจริงข้อนี้ดูจากกราฟแล้วก็ตอบได้เลย แต่ผมขอคิดแบบ algebric ดีกว่า (เรียกแบบนี้รึเปล่า อิอิ)

คูณตลอดด้วย $\large \sin \frac{\pi}4=\cos \frac{\pi}4>0$

$$\sin x \cos \frac{\pi}4- \cos x \sin\frac{\pi}4<0$$
$$\sin (x-\frac{\pi}4)<0$$
นั่นคือ $\large x-\frac{\pi}4 \in(-\pi+2n\pi,2n\pi)\quad,n\in I$
นั่นคือ $\large x \in( (2n-\frac 34)\pi,(2n+\frac 14)\pi)\quad,n\in I$

หุหุ ไหนๆทำข้อนี้แล้ว เอากราฟมาให้ดูดีกว่า

หมายเหตุ สีเขียวเป็นกราฟของ $\cos$ สีฟ้าเป็นกราฟของ $\sin$
จุดที่ $\large \sin x=\cos x$ คือ $\frac{\pi}4+n\pi$
ก็จะได้คำตอบเดียวกันครับ คือ
$\large x \in( (2n-\frac 34)\pi,(2n+\frac 14)\pi)\quad,n\in I$

ขอใช้สิทธิ์ตั้งคำถามข้อต่อไปละกันครับ

สามเหลี่ยมที่มีด้านทั้งสามยาว $$\large \sin \theta,\sin 2\theta,\sin 3\theta\qquad,0\leq \theta <2\pi$$
$(i)\ \ $ มีพื้นที่เท่าไหร่ครับ
$(ii)\ \ $ มีพื้นที่มากที่สุดเท่าไหร่ครับ

(from mathlinks)

ข้อนี้ผมใช้คอมพิวเตอร์ช่วยคำนวณได้มันหยดเลยครับ ได้ผลดังนี้

1. พื้นที่ของสามเหลี่ยมคือ $$\frac{\sin \theta \sin 2\theta \sin 3\theta}{2}$$
2. พื้นที่มากที่สุดคือ $$\frac{34\sqrt2+ 5\sqrt5}{216}$$
ไม่เข้าใจเหมือนกันครับว่า ทำไมคำตอบของข้อ 1. มันออกมาได้พอดิบพอดีอย่างงั้น :rolleyes:

ข้อ 1 ถูกต้องแล้วครับ ส่วนข้อ 2 ยังไม่ทราบเหมือนกันครับ
และข้อ 1 ถ้าอยากดูแนวคิดก็ ที่นี่เลยครับ
Area of triangle

ได้คำตอบ $ \frac{34\sqrt2+ 5\sqrt5}{216} $ เท่ากับพี่ warut ครับ

ให้ $ x=\sin\theta $ และพิจารณา
$ g(x)=\frac{1}{2}\sin\theta\sin 2\theta\sin 3\theta=x^3(3-4x^2)\sqrt{1-x^2} $
เมื่อ $ x\in\left(0,\frac{\sqrt3}{2}\right) $
หาอนุพันธ์ของ $g(x)$ จะได้ว่าค่าสูงสุดอยู่ที่ $ x^2=\frac{8-\sqrt{10}}{12} $
จะได้พื้นที่สามเหลี่ยมมากที่สุดคือ $ \frac{34\sqrt2+ 5\sqrt5}{216} $ ตารางหน่วย โดยเกิดสมการเมื่อ $ \sin^2\theta=\frac{8-\sqrt{10}}{12} $

แหะๆ วิธีไม่ค่อยสวยงามเท่าไหร่ มีใครมีวิธีอื่นอีกรึเปล่าครับ

ผมก็ทำคล้ายๆกันนี่แหละครับ แต่ผมหาจุดสูงสุดของ $\{g(x)\}^2$ แทน $g(x)$ ซึ่งอาจช่วยให้ง่ายขึ้นเล็กน้อยครับ (ไม่ต้องติด square root)

16. จงหาจำนวนจริง x ที่สอดคล้องกับสมการ
$$4^{3x+2}-3\cdot 4^{x+1}+4^{\log_{16}5}=1$$

สมการนี้สมมูลกับ $$4\cdot4^{3x}-3\cdot4^x=\frac{1-\sqrt5}{4}$$ ให้ $\cos y=4^x$ ดังนั้นจะได้ $\cos 3y=\frac{1-\sqrt5}{4}$ หรือ $y=\frac{\pi}{3}(2n+1\pm\frac{2}{5})$ ซึ่งจะได้ $4^x=\cos(\frac{\pi}{3}(2n+1\pm\frac{2}{5}))$ โดยเงื่อนไขของฟังก์ชัน log จะได้คำตอบเป็น $x=\frac{1}{2}\log_2(\cos((2n\pm\frac{1}3\pm\frac{2}{5})\pi))$ เมื่อ n เป็นจำนวนเต็ม

หากผิดตรงไหนช่วยระบุด้วยครับ อ้อหากไม่ลำบากช่วยเฉลยละเอียดข้อ 10 ด้วยครับ

เฉลยข้อ 10 โดยคุณ GFK



ถูกต้องแล้วครับ

เชิญตั้งข้อใหม่เลยครับ

17. สูตรประมาณผลคูณของ Vieta (Vieta's Product approximation) ได้มาจาก $$1=\frac{\pi}{2} \cdot\frac{\sqrt{2}}{2} \cdot\frac{\sqrt{2+\sqrt{2}}}{2} \cdot\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\cdots$$ จงพิสูจน์สูตรด้านบนนี้โดยอาศัยข้อเท็จจริงที่ว่า $$\sin x=2\sin\frac{x}{2}\cos\frac{x}{2}\quadและ\quad\frac{\sin x}{2^n\sin\frac{x}{2^n}}=\prod_{k=1}^n\cos\frac{x}{2^k}$$ และใช้ผลที่ได้แสดงว่า $$\frac{2}{\pi}=\prod_{n=2}^{\infty}\cos\frac{\pi}{2^n}$$
ใบ้: l'Hospital และสูตรครึ่งมุมโคไซน์

เนื่องจาก cosine มีค่า periodic และเราต้องการคำตอบที่ $\cos y>0$ เท่านั้น ดังนั้นจริงๆแล้ว สมการนี้มีคำตอบเพียง 2 คำตอบเท่านั้นคือ $$ x= \frac12 \log_2 \cos \frac{\pi}{5} = \frac12 \log_2 (1+ \sqrt5) -1 $$ และ $$ x= \frac12 \log_2 \cos \frac{7\pi}{15} = \frac12 \log_2 \left( \sqrt{30- 6\sqrt5} -\sqrt5 -1 \right) -\frac32 $$