คุณ TOP เคยแสดงวิธีทำโจทย์แบบเดียวกันนี้อย่างเหนือชั้นไว้เมื่อนานมาแล้วครับ

ครับสุดยอดจริงๆสำหรับแนวคิด เอาเป็นว่าผมขอเสนอวิธีของผมด้วยละกัน

ให้ \(a_n\) แทนเทอมที่ต้องการหาลิมิต จะเห็นได้ว่า \(a_n\) เป็นลำดับเพิ่ม และยิ่งกว่านั้น \(a_n<3\) เนื่องจากหากแทนพจน์ \(\sqrt{1+n}\) ด้วย \(1+n\) ในสูตรของ \(a_n\) ค่าที่ได้(ซึ่งเพิ่มขึ้น) จะเท่ากับ 3 พอดี ดังนั้นลำดับ \(a_n\) ลู่เข้า และ \(\lim_{n\to\infty}a_n\leq3\)

พิจารณาลำดับ
\[
b_N=\sqrt{1+N\sqrt{1+(N+1)\sqrt{1+\cdots}}}
\]
ซึ่งพิสูจน์ได้ทำนองเดียวกับข้างบนว่า \(b_N\) ลู่เข้า จะเห็นว่าถ้าตัด 1 ออกจากสูตรของ \(b_N\) ค่าที่ได้จะน้อยลง ดังนั้น
\[
b_N\geq\sqrt{N\sqrt{(N+1)\sqrt{(N+2)\sqrt{\cdots}}}}\geq\sqrt{N(N+1)}
\]

ดังนั้นเราได้ว่า
\[
\lim_{n\to\infty}a_n=\sqrt{1+2\sqrt{1+3\sqrt{1+\cdots\sqrt{1+(N-1)b_N}}}}
\]

แต่เนื่องจาก \(\sqrt{N(N+1)}=O(N+1)\) เมื่อ \(N\) มากๆ และ หากแทนพจน์ \(b_N\) ด้วย \(N+1\) ค่าที่ได้เท่ากับ 3 พอดี ดังนั้นเราสรุปได้ว่า \(\lim_{n\to\infty}a_n\geq3\)

อืมผมคิดผิดจริงๆด้วยนั่นแหละครับคุณ aaaa
ส่วนข้อ 12 นี่ยังง่ายจริงๆด้วยครับ งั้นผมเพิ่มเงื่อนไขเป็น x>5 แล้วกันนะครับเพื่อขจัด trivial solution ไป จริงๆข้อนี้อยากให้รู้จักเอกลักษณ์ที่น่าสนใจเกี่ยวกับ factorial น่ะครับ สวยดี

เฉลยข้อ 12
ให้ \(y=x!-1,\,z=x!\)

กรณีทั่วไปของข้อ 13
ให้ \(n\geq3\) เป็นจำนวนจริงใดๆ จงพิสูจน์ว่า ถ้า \(a,b,c>0\) และ \(abc=1\) แล้ว
\[
\frac{1}{a^n(b+c)}+\frac{1}{b^n(c+a)}+\frac{1}{c^n(a+b)}\geq\frac{3}{2}
\]

อืมผมเพิ่งจะพบว่าโจทย์ข้อนี้มีคนทำไปแล้วในเวปอื่น
ขออนุญาตินำเสนอวิธีที่เขานำเสนอครับ

ให้ \(x=1/a,\,y=1/b,\,z=1/c\) จะได้อสมการสมมูลกับ
\[
\frac{x^{n-1}}{y+z}+\frac{y^{n-1}}{z+x}+\frac{z^{n-1}}{x+y}\geq\frac{3}{2}
\]
เนื่องจากอสมการสมมาตรเมื่อสลับลำดับ (cyclic) เราสามารถสมมติว่า \(x\leq y\leq z\) ดังนั้นโดยอสมการ Chebyshev จะได้ว่า
\[
\frac{x^{n-1}}{y+z}+\frac{y^{n-1}}{z+x}+\frac{z^{n-1}}{x+y}\geq\frac{1}{3}\left(x^{n-2}+y^{n-2}+z^{n-2}\right)\left(\frac{x}{y+z}
+\frac{y}{z+x}+\frac{z}{z+y}\right)
\]
เทอมแรกใช้อสมการ Power-Mean และอสมการ AM-GM ได้ว่า
\[
\left(x^{n-2}+y^{n-2}+z^{n-2}\right)\geq(x+y+z)^{n-2}/3^{n-3}\geq\frac{3^{n-2}}{3^{n-3}}=3
\]
เทอมที่เหลือใช้อสมการ Cauchy

เยี่ยมครับ. ได้คุณ aaaa มาเล่นอีกคนครึกครื้นขึ้นเยอะเลย คิดเร็วมาก ๆ เลยครับ. อย่างกับซุบเปอร์ไซยา เรื่องอสมการเราเคยเล่นกันมาบ้างแล้วครับ. ในกระทู้นี้ โจทย์อสมการ

นี่โจทย์เก่าครับ. ขุดขึ้นมาเขียนแบบ Latex ใหม่
สำหรับทุกจำนวนจริงบวก \(a,b,c\) โดยที่ \(abc = 1\) จงพิสูจน์ว่า
\[\frac{a^3b^3}{a^7+b^7+a^3b^3} + \frac{b^3c^3}{b^7+c^7+b^3c^3} + \frac{c^3a^3}{c^7+a^7+c^3a^3} \leq 1\]

ขอบคุณครับคุณ gon ตั้งแต่รู้จักเวปนี้สนุกมากครับ
มีประโยชน์มากเลยครับอยากให้เวปนี้อยู่ตลอดไปครับ
จะได้เป็นแหล่งแลกเปลี่ยนความรู้ด้าน math ของคนไทย

ข้อกรณีทั่วไปของ ข้อ 13. ผมเสนอแนวคิดซึ่งสลับนิดหน่อยกับของเก่าดังนี้ครับ.
หลังจากจัดรูป \(LHS.\) ได้เป็น
\[\frac{x^{n-1}}{y+z} + \frac{y^{n-1}}{z+x} + \frac{z^{n-1}}{x+y}\]
จากนั้นทำแบบนี้ต่อคือ โดยโคชี \(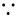
(LHS.)[ (y+z) + (z+x) + (x+y) ] \geq (x^{\frac{n-1}{2}} + y^{\frac{n-1}{2}} + + z^{\frac{n-1}{2}})^2\)
\
\[LHS. \geq \frac{(x^{\frac{n-1}{2}} + y^{\frac{n-1}{2}} + z^{\frac{n-1}{2}})^2}{2(x+y+z)} \geq \frac{(x+y+z)^2}{2(x+y+z)} = \frac{x+y+z}{2} \geq \frac{3}{2}\sqrt[3]{xyz} = \frac{3}{2}\]

เพราะเมื่อ \(x, y, z > 0, xyz = 1, m \geq 1\)
\[x^m + y^m + z^m \geq x + y + z\]
เพราะ โดย Chebyshev
\(x^m + y^m + z^m \geq \frac{(x^{m-1}+y^{m-1}+z^{m-1})(x+y+z)}{3} \geq \sqrt[3]{(xyz)^{m-1}}(x+y+z) = x + y + z\)

เยี่ยมจริงๆครับคุณ gon โดยเฉพาะอสมการรองสุดท้าย

โอ ขายดีเป็นเทน้ำเทท่าและแฮะ ผมว่าคุณ aaaa น่าจะเป็น ซุปเปอร์ไซย่าขั้นที่ 5 แล้วนะพี่กร :D คิดเร็วมากๆ ตามความคิดผมทันหมดเลย :)

เติมโจทย์อสมการให้อีกข้อครับ

14. ให้ a,b,c เป็นจำนวนจริงบวกซึ่ง a+b+c+abc = 1
(i) จงพิสูจน์ว่า \[ \sqrt[3]{ab+bc+ca} + \sqrt[3]{abc} \leq 1 \]
(ii) ถ้า a,b,c ทำให้สมการในข้อ (i) เป็นจริง จงพิสูจน์ว่า abc < \( \frac{1}{16} \)

ข้อ 14 อันแรกวิธีของผมยาวมากๆ อยากให้คุณ nooonuii ช่วยเฉลยวิธีสั้นๆหน่อยครับ
ส่วนข้อสองนี่ง่ายครับ เป็นจริงเสมอ จากอสมการ AM-GM
\[ 4\sqrt[4]{abc(abc)}\leq a+b+c+abc=1 \]
และสังเกตุว่ามันไม่มีทางเป็นเท่ากับได้ เพราะว่า \( 0<a,b,c<1 \)

PS จริงๆแล้วได้มากกว่านั้นคือ \( abc\leq1/27 \)

โอ...ผมว่าข้อนี้ง่ายที่สุดในบรรดาโจทย์อสมการทั้งหมดแล้วนะครับเนี่ย ผมสร้างโจทย์ข้อนี้จาก (1-a)(1-b)(1-c) = ab+bc+ca ครับ :)

อืม... บางทีมุมมองของคนคิดโจทย์กับคนแก้ปัญหาโจทย์ก็ไม่เหมือนกันครับ :)

ส่วนที่ทำให้น้อยลงได้เนี่ยก็ไม่ทราบเหมือนกันครับว่าจะลงไปได้ถึงไหน ใครหา upper bound ได้ดีกว่าของคุณ aaaa ช่วยเอามาบอกด้วยครับ

ว้าว ผมคิดไม่ถึงจริงๆ อืมแต่ผมได้อสมการที่ sharp กว่าเดิมครับ
จงแสดงว่า
\[
ab+bc+ca\leq\frac{(2+abc)(1+2abc)}{7-abc}
\]