ตรีโกณ ความคล้าย สหายสามเหลี่ยม
 

$\qquad \quad $ :kiki: หอเอนเมืองปิซา ตั้งอยู่ที่เมืองปิซาประเทศอิตาลี เป็นหนึ่งในเจ็ดสิ่งมหัศจรรย์ของโลกยุคกลาง หอเอนปิซาเป็นหอคอย 8 ชั้นทำด้วยหินอ่อนมีลักษณะเอียงเหมือนกับจะโค่นล้ม ใช้เวลาสร้างนานถึง 176 ปี ตั้งแต่ พ.ศ. 1717 ถึง 1893 เป็นสถานที่สำคัญในการทดสอบทฤษฎีของกาลิเลโอที่ว่า "เมื่อปล่อยวัตถุที่มีน้ำหนักต่างกันพร้อมกัน จากที่สูงระดับเดียวกัน ผลที่ได้คือวัตถุจะตกถึงพื้นเวลาเดียวกัน" ซึ่งเป็นการลบล้างความเชื่อเดิมตามทฤษฎีของอริสโตเติลที่ว่า "ผลที่ได้คือวัตถุที่มีน้ำหนักมากกว่า จะตกถึงพื้นก่อนวัตถุที่มีน้ำหนักเบากว่า" โดยกาลิเลโอได้นำก้อนโลหะสองก้อน หนัก 10 ปอนด์และ 20 ปอนด์ ไปทดลองปล่อยลงมาพร้อมกันจากหอเอน ปรากฏว่าก้อนโลหะทั้งสองตกถึงพื้นพร้อมกัน!! :eek:
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad $
$\qquad \quad $ :sung:กาลิเลโอ (Galileo : พ.ศ. 2103 - 2186) เกิดที่เมืองปิซา เป็นทั้งนักวิทยาศาสตร์ นักคณิตศาสตร์ และนักดาราศาสตร์ มีผลงานที่สำคัญ เช่น เป็นผู้ค้นพบกฎการแกว่งของลูกตุ้มกฎเกี่ยวกับความเร็วของวัตถุเมื่อตกจากที่สูงและพบจุดดับบนดวงอาทิตย์ เป็นผู้ประดิษฐ์กล้องโทรทรรศน์ นาฬิกาน้ำ ไม้บรรทัดและเทอร์โมมิเตอร์ กาลิเลโอจะไม่ยอมเชื่อทฤษฎีต่างๆ ที่ได้เผยแพร่ทั้งในอดีตและปัจจุบันจนกว่าจะได้มีการตรวจสอบด้วยตัวเองและจากการที่กาลิเลโอเป็นผู้ที่ศึกษาศาสตร์หลายสาขาจนมีความเชี่ ยวชาญ จึงทำให้สามารถเชื่อมโยงศาสตร์ต่างๆ เข้าด้วยกัน ก่อให้เกิดผลงานมากมาย
$\qquad \quad $ :D ในการทดลองครั้งหนึ่ง กาลิเลโอปล่อยก้อนโลหะจากตำแหน่งบนหอคอยซึ่งสูงตามแนวของหอคอย 55 เมตร ปรากฏว่าก้อนโลหะตกถึงพื้นในตำแหน่งที่อยู่ห่างจากฐานของหอคอย 4.8 เมตร อยากทราบว่าหอเอนเอียงจากแนวตั้งประมาณกี่องศา :huh: :huh:

เขียนบทความน่าสนใจดีครับ ใช้เป็นประเด็นคำถามโยงเข้าสู่โจทย์ตรีโกณมิติง่ายๆได้ แต่หากเว้นวรรคบ่อยกว่านี้นิดนึงจะอ่านง่ายกว่านี้ครับ

รูปประกอบสวยดีครับ... :great: แต่ผมว่านะ ถ้าจับเวลาแบบเป๊ะจริง ๆ จะตกถึงพื้นไม่พร้อมกัน :rolleyes:

$ \qquad \qquad $มาอีกแล้วครับท่าน คือโจทย์นี้มีเพื่อนผู้เป็นเลิศที่สุดในห้องเรียนของผมคิดขึ้น เขาเกิดอาการคลั่งในตรีโกณมิติขึ้นมา เขาเอามาถามผม แต่ผมตอบเขาไม่ได้ เลยอยากลองมาถามพี่ๆ ดูครับ
$ \qquad \qquad $ :o ตรีโกณข้อแรกกับข้อ 2 ครับ$\;$กำหนดให้ tan A = $\frac{\displaystyle{ 3 }}{\displaystyle{ 7 }}$ จงหาค่าของ $\frac{\displaystyle{ 2\;sin\;A\;cos\;A-cos\;A }}{\displaystyle{ 1-\;sin\;A\;+\;sin^2\;A-\;cos^2\;A }} $
$ \qquad \qquad $ :rolleyes: จงหาค่า A จากสมการ เมื่อ $ \displaystyle{ 0 ^\circ < A < 90^ \circ }; \quad 4 \; cos\; A = 3 \;sec\; A $
$ \qquad \qquad $ :D ความคล้ายข้อ 3 ครับ$\;$จากรูป AB เป็นเส้นผ่านศูนย์กลางที่มี O เป็นจุดศูนย์กลางของวงกลม ถ้า AB = 10, AC = 6 และ OE$ \bot $BC ที่ E จงหาความยาวของ DE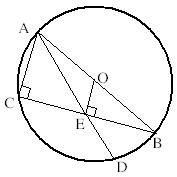

หากสงสัยวิธีทำถามได้นะครับ

แล้วคิดยังไงถึงได้คำตอบนี้เหล่านี้ล่ะครับ (ขอโทษที่รบกวนครับ :sweat: :cry: )

เมื่อปีพ.ศ. 2540 เคยมีคำถามนี้ปรากฏในการสอบแข่งขันอะไรสักอย่าง แต่ผมจำไม่ได้ :sweat: จำได้แค่ว่าเคยเห็นตอนปี 40 ตอนนั้นผมยังเป็นเด็กประถมอยู่ เลยไม่อยากเก็บมาคิด แต่พอกลับมาดูอีกครั้ง มันน่าสนใจดี แต่ก็คิดไม่ออกสักทีครับ เห็นโจทย์แล้วตาลายครับ :died:
กำหนด $\sin^2A\;+\;\cos^2A\:=\:1$ เมื่อ $0^\circ\:\leq\:A\:\leq\:90^\circ$ และ $\sin\:90^\circ\:=\:1$
จงหาค่าของ $\sin^22^\circ\;+\;\sin^24^\circ\;+\;\sin^26^\circ\;+\;\sin^28^\circ\;+\;...\;+\;\sin^290^\circ$

ไหนๆ ก็มาแล้ว งั้นขอแถมคนที่ชอบคิดโจทย์แนวนี้ละกันครับ

- ค่าของ $3tan^2\frac{\pi}{6}+\frac{4}{3}cos^2\frac{\pi}{6}-4cos^2\frac{\pi}{4}-\frac{2}{3}sin^2\frac{\pi}{3}$ เท่ากับเท่าไร (ปรากฏไว้เมื่อปี พ.ศ. 2543)

- ถ้า $\displaystyle{\frac{\sin x +\sin y +\sin z}{\sin(x+y+z)}\:=\:\frac{\cos x +\cos y +\cos z}{\cos(x+y+z)}\:=\:2}$ แล้ว จงหาค่าของ $\sin x\,\sin y +\sin y\,\sin z +\sin z\,\sin x$ (ปรากฏไว้เมื่อปี พ.ศ. 2547)

- ถ้า $w$ เป็นรากที่สามของ $4\sqrt{2}(-1 + \dot \imath)$ และเป็นรากที่สี่ของ $8\left(1-\sqrt{3}\dot \imath\right)$ แล้ว $w$ เท่ากับข้อใดต่อไปนี้

1. $2\left(\cos\frac{3\pi}{12} + \dot \imath \sin\frac{3\pi}{12}\right)$
2. $2\left(\cos\frac{5\pi}{12} + \dot \imath \sin\frac{5\pi}{12}\right)$
3. $2\left(\cos\frac{11\pi}{12} + \dot \imath \sin\frac{11\pi}{12}\right)$
4. $2\left(\cos\frac{13\pi}{12} + \dot \imath \sin\frac{13\pi}{12}\right)$

(ปรากฏเมื่อปี พ.ศ. 2547 เช่นกัน)
(ขอขอบพระคุณตำราพงศาวดารคณิตศาสตร์ อิ..อิ... :happy: )

มาขยายความคำตอบก่อนครับ

ข้อสอง ได้มาจาก
$$\frac{ 2\sin A\cos A-\cos A }{1-\sin A+\sin^2 A-\cos^2 A}=
\frac{\cos A(2\sin A-1)}{\underbrace{2\sin^2 A-\sin A}_{=\sin A(2\sin A-1)}}=\cot A$$
ข้อสาม คูณสมการตลอดด้วย cos A หารด้วยสี่แล้วถอดรากจะได้ $\cos A=\frac{\sqrt3}{2}$ จากเงื่อนไข 0°<A<90° จะได้ A=30°

ข้อสี่ เราทราบว่า OE ตั้งฉากและแบ่งครึ่งคอร์ด BC โดยพีทากอรัสจะได้ BC=8, AE=$\sqrt{52}$ หากลองลาก DB จะได้ $\Delta ACE~\Delta DEB$ นั่นคือ AE:EB=CE:ED แทนค่าแล้วแก้หา ED ก็จะได้คำตอบครับ

ตอบอีกสามข้อละกัน

$\displaystyle\sum_{n=1}^{45} \sin^2 (2n)°=23$

$3\tan^2\frac{\pi}{6}+\frac{4}{3}\cos^2\frac{\pi}{6}-4\cos^2\frac{\pi}{4}-\frac{2}{3}\sin^2\frac{\pi}{3}=-\frac{1}{2}$

$w=w^4/w^3=2\text{cis}(\frac{11\pi}{12})$

ขอพิมพ์วิธีทำข้อนี้แยกต่างหาก ผมไม่ค่อยชัวร์นะครับ ใครเจอที่ผิดหรืออยากเสนอแนะอะไรบอกกันด้วยนะครับ

จาก $\displaystyle\frac{\sin X+\sin Y+\sin Z}{\sin (X+Y+Z)}=\frac{\cos X+\cos Y+\cos Z}{\cos (X+Y+Z)}=2$
คูณไขว้แล้วจัดรูปจะได้ $\sum_{cyc}\sin(X+Y)=0$ ...(i)
จาก $(\sum_{cyc}\sin X)^2+(\sum_{cyc}\cos X)^2=2[\sin^2(X+Y+Z)+\cos^2(X+Y+Z)]=2$
จะได้ $\sum_{cyc}(\cos X\cos Y+\sin X\sin Y)=\sum_{cyc}\cos(X-Y)=1/2$ ...(ii)
หรือ $\sum_{cyc}\cos(X+Y)=1/2-2\sum_{cyc}\sin X\sin Y$ ...(ii)'
(i)²+(ii)'² จะได้
$\begin{array}{ll}
&3+2\sum_{cyc}[(\cos (X+Y)\cos (X+Z)+\sin (X+Y)\sin (X+Z)]\\
=&3+2\sum_{cyc}\cos(X-Z)=4
=\frac{1}{4}-2\sum_{cyc}\sin X\sin Y+4(\sum_{cyc}\sin X\sin Y)^2\\
\end{array}$
แก้สมการหา $\sum_{cyc}\sin X\sin Y$ จะได้คำตอบเป็น -3/4 หรือ 5/4

ข้อนี้เคยตอบไปแล้วที่นี่ ครับ