
 |
Theory of Equations
 |
 |
ข้อ 2) สมมติให้ x = w เมื่อ w เป็นรากที่ 3 ของ 1 ตัวแรก กล่าวคือ $1+w+w^2 = 0, w^3 = 1$
โจทย์บอกว่า n เป็นจำนวนคี่(บวก) ที่หารด้วย 3 ไม่ลงตัว แสดงว่า n = 6k + 1 หรือ 6k + 5 สำหรับทุกจำนวนเต็มบวก k รวมศูนย์ แทน x = w ลงในพหุนามที่ให้มาจะได้ว่า $(1+x)^n - x^n - 1 = (1 + w)^n - w^n - 1 = (-w^2)^n - w^n - 1$ $= -(w^{2n} + w^n + 1)$ กรณีที่ n = 6k + 1 ; $= -(w^{2n} + w^n + 1) = -(w^{12k+2} + w^{6k+1} + 1)$ $=-(w^2 + w + 1) \quad (\because w^3 = 1) = 0$ กรณีที่ n = 6k + 5 ก็ทำนองเดียวกัน ดังนั้น x - w จะเป็นตัวประกอบของพหุนามดังกล่าว *** ในทำนองเดียวกัน จะสามารถแสดงได้ว่า ถ้าสมมติให้ $x = w^2$ ก็จะได้ว่า พหุนามที่โจทย์ให้มามีค่าเท่ากับศูนย์ ดังนั้นทั้ง $x - w$ และ $x - w^2$ จะเป็นตัวประกอบของพหุนามที่ให้มา แต่ $(x - w)(x-w^2) = x^2 - (w+w^2)x + w^3 = x^2 - (-1)x + 1$ นั่นคือ $(1+x)^n - x^n - 1$ จะหารด้วย $x^2 + x + 1$ ทุกจำนวนเต็มคี่บวกที่หารด้วย 3 ไม่ลงตัว ;) |
ข้อ 1 $\because \quad (x-a-\sqrt{b} )(x-a+\sqrt{b}) = (x-a)^2 - b$
สมมติให้ f(x) หารด้วย $(x-a)^2 - b$ แล้วเหลือเศษ cx + d $\therefore \quad f(x) = ([(x-a)^2 - b])Q(x) + cx + d$ โดยสมมติฐาน $f(a + \sqrt{b}) = 0$ ดังนั้น $f(a + \sqrt{b}) = 0\cdot Q(x) + c(a + \sqrt{b}) + d = 0$ นั่นคือ $ca + c\sqrt{b} + d = 0$ แต่ $\sqrt{b}$ เป็นจำำนวนอตรรกยะ แสดงว่าทั้ง $c\sqrt{b}$ และ $ca + d = 0$ นั่นคือ c = 0 และ d = 0 ดังนั้น f(x) จะมี $(x-a)^2 - b = (x-a-\sqrt{b} )(x-a+\sqrt{b})$ เป็นตัวประกอบ แสดงว่า $a - \sqrt{b}$ จะเป็นรากของพหุนาม f(x) ด้วย ;) |
สำหรับ ข้อ 3 นี่ง่ายที่สุดครับ
สมมติให้ f(x) = Q(x)(x-a)(x-b) + cx + d แต่ f(a) = 0 และ f(b) = 0 ดังนั้น ca + d = 0 และ cb + d = 0 ดังนั้น ca - cb = 0 แล้ว c(a-b) = 0 แต่ a ไม่เท่ากับ b แสดงว่า c = 0 ทำให้ได้ว่า d = 0 ด้วย ดังนั้น f(x) = Q(x)(x-a)(x-b) แสดงว่า (x-a)(x-b) เป็นตัวประกอบของ f(x) :D |
ขอถามมั่งนะครับ
4. ถ้า a<b<c เป็นรากที่เป็นจำนวนจริงของสมการ $\ x^3+px^2+3x-10\ =\ 0\ $ จงหาค่าของ p เอ...อ่านโจทย์แล้วผมก็ขีดๆเขียนๆได้เท่านี้อะครับ a+b+c = -p ab+ac+bc =3 abc = 10 $(a+b+c)^2\ =\ a^2+b^2+c^2+2(ab+ac+bc)$ $p^2\ =\ a^2+b^2+c^2+6$ $a^2+b^2+c^2\ =\ p^2-6$ แล้วผมก็แว๊บไปเปิดหนังสือ หาเอกลักษณ์ครับ ได้ดังนี้ $a^3+b^3+c^3-3abc\ =\ (a+b+c)(a^2+b^2+c^2-ab-ac-ca)$ $a^3+b^3+c^3-30\ =\ (-p)(p^2-6-3)$ $a^3+b^3+c^3\ =\ -p^3+9p+30$ แล้วก็งงต่อไปครับ :D |
อ้างอิง:
|
คุณ warut คิดเหมือนผมเลยครับ ใจผมข้อนี้อยากให้ตัวท้ายสุดเป็นเลข 10 จริง ๆ เพราะถ้ามันเป็น 10 ก็จะจบเลยทันที ขอถามอีก 1 เสียงครับ เอามาจากหนังสือเล่มไหนเอ่ย :rolleyes:
|
เอาโจทย์มาจาก หนังสือที่เรียนตอนเข้าค่าย 1 สอวน. ศูนย์ภาคใต้ (ไม่รู้มีตอนล่างรึเปล่า) ครับ
อยู่ในเรื่อง เอกลักษณ์ , พหุนาม :D เดี๋ยวผมลองติดต่อ อ. ดูนะครับ ว่าโจทย์ถูกต้องรึเปล่า (หรือเดี๋ยวถามน้อง Tony ดีกว่า มีประสบการณ์ตั้ง 2 ปีแล้ว :cool: ) |
อ้อ...มีอีกข้อนึงครับ ที่อยู่ในเล่มเดียวกัน ทำนองเดียวกันด้วย
5.กำหนดให้ x<y<z จงแก้ระบบสมการ x + y + z = 6 xy + zy + zx = 11 xyz = 6 ข้อนี้ผมเอาไปเขียนเป็นสมการ $a^3-6a^2+11a-6=0$ แล้วผมหารสังเคราะห์ แยกตัวประกอบได้ $(a-1)(a-2)(a-3)=0$ นั่นคือ a = 1,2,3 x = 1 y = 2 z = 3 นั่นเองครับ :D |
ถ้าเป็นข้อข้างบนนี่ก็ตรง ๆ ครับ ไม่มีอะไร แต่ถ้าเป็นข้อที่ว่านี่ จากการคาดเดา ถ้าใช้ criterion ว่ารากทั้งสามจะจะเป็นจำนวนจริงแตกต่างเมื่อใดนั้น มันก็สมควรจะได้คำตอบออกมาเป็นช่วง มากกว่าได้ค่าเดี๋ยว ๆ นะครับ. :)
|
อ้างอิง:
แทนค่า \(y=x-p/3\) ลงในสมการโจทย์เพื่อกำจัดเทอมกำลังสอง เราจะได้สมการใหม่คือ\[y^3+ (3-\frac{p^2}{3})y+(\frac{2}{27}p^3-p-10)=0\]ดังนั้นเราต้องการให้\[-4 (3-\frac{p^2}{3})^3-27(\frac{2}{27}p^3-p-10)^2=40p^3+9p^2-540p-2808> 0\]หลังจากแก้สมการกำลังสามอันใหม่ เราจะได้คำตอบคือ\[p>\frac{3}{40} (-1+3\sqrt[3]{3037+880\sqrt{11}}+3\sqrt[3]{3037-880\sqrt{11}})= 5.108166\dots\]ครับผม :) |
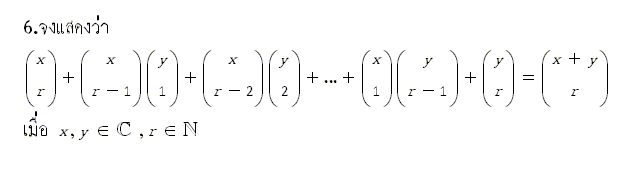 |
 |
อ้างอิง:
สมมติว่ามีของทั้งหมดอยู่ 2 กอง กองละ x ชิ้น และ กองละ y ชิ้น โดยต้องการเลือกมาทั้งหมด r ชิ้น ถ้าเลือกโดยไม่มีเงื่อนไข จะทำได้ ${x+y \choose r}$ วิธี ซึ่งสามารถแบ่งวิธีการเลือกของ ได้อีกอย่าง เป็นกรณี ๆ คือ กรณีที่ 1 : เลือกของจากของ x ชิ้น มา r ชิ้น เลือกของจากกอง y ชิ้น มา 0 ชิ้น ทำได้ ${x \choose r}{y \choose 0}$ วิธี กรณีที่ 2 : เลือกของจากของ x ชิ้น มา r - 1 ชิ้น เลือกของจากกอง y ชิ้น มา 1 ชิ้น ทำได้ ${x \choose r - 1}{y \choose 1}$ วิธี ........... กรณีที่ r + 1 : เลือกของจากของ x ชิ้น มา 0ชิ้น เลือกของจากกอง y ชิ้น มา r ชิ้น ทำได้ ${x \choose o}{y \choose r}$ วิธี จับทุกกรณีมาบวกกันก็จะได้ตามที่ต้องการพิสูจน์ :cool: |
| เวลาที่แสดงทั้งหมด เป็นเวลาที่ประเทศไทย (GMT +7) ขณะนี้เป็นเวลา 04:54 |
Powered by vBulletin® Copyright ©2000 - 2024, Jelsoft Enterprises Ltd.
Modified by Jetsada Karnpracha