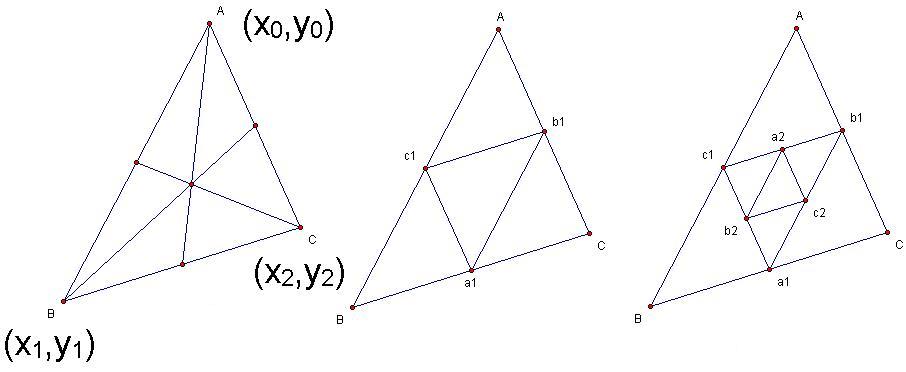
1)With an easily proof we'll find out that the centroid of any triangle
is the same point with it's medial triangle's centroid.

So now, We'll let $a_0,b_0,c_0$ be the midpoints of $a,b,c$ respectively
and also let $a_{n+1},b_{n+1},c_{n+1}$ be the midpoints of opposite side of $a_n,b_n,c_n$
$\displaystyle{\because a_{n+1}=\frac{b_n+c_n}{2},b_{n+1}=\frac{c_n+a_n}{2},c_{n+1}=\frac{a_n+b_n}{2}}$
$\rightarrow a_{n+1}+b_{n+1}+c_{n+1}=a_n+b_n+c_n,A+B+C=a_n+b_n+c_n$
If we continue drawing a medial triangle again and again we'll get $a_n=b_n=c_n=¢roid

$\therefore$coordinate of the centroid is $\displaystyle{\lim_{n\rightarrow\infty}} \frac{a_n+b_n+c_n}{3} = \frac{A+B+C}{3} = \left(\left(\frac{x_0+x_1+x_2}{3}\right), \left(\frac{y_0+y_1+y_2}{3}\right)\right)$