
 |
|
|||||||
| สมัครสมาชิก | คู่มือการใช้ | รายชื่อสมาชิก | ปฏิทิน | ข้อความวันนี้ | ค้นหา |
  |
|
|
เครื่องมือของหัวข้อ | ค้นหาในหัวข้อนี้ |
|
#1
|
|||
|
|||
|
ขอ เท้าความขากคราวที่แล้วนะครับ
จากกระทู้ ข้อสอบสมาคมครับ(ม.ต้น) ของปีที่แล้ว ปีนี้ผมขอรับหน้าที่เอาข้อสอบมาลงตามธรรมเนียมอีกเชนเคยครับ  (ปีนี้อยากบอกว่า ผมผิดข้อง่ายๆอะ คิดแล้วเจ็บใจ T_T)      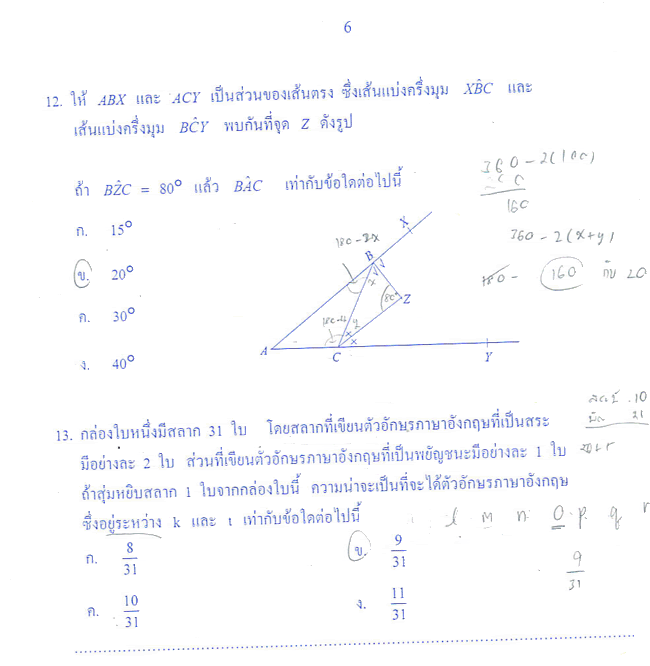
__________________
[[:://R-Tummykung de Lamar\\::]] || (a,b,c > 0,a+b+c=3) $$\sqrt a+\sqrt b+\sqrt c\geq ab+ac+bc$$ 16 มกราคม 2006 20:03 : ข้อความนี้ถูกแก้ไขแล้ว 2 ครั้ง, ครั้งล่าสุดโดยคุณ R-Tummykung de Lamar |
|
#2
|
|||
|
|||
 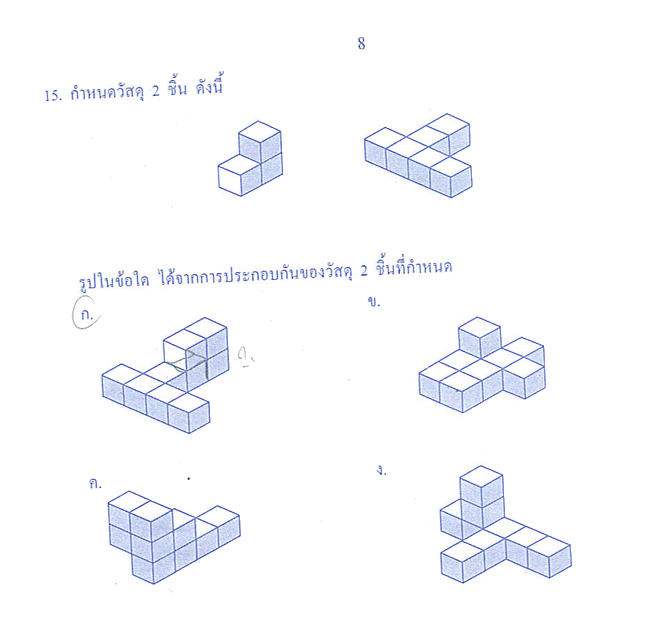 ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| ตอนที่ 2 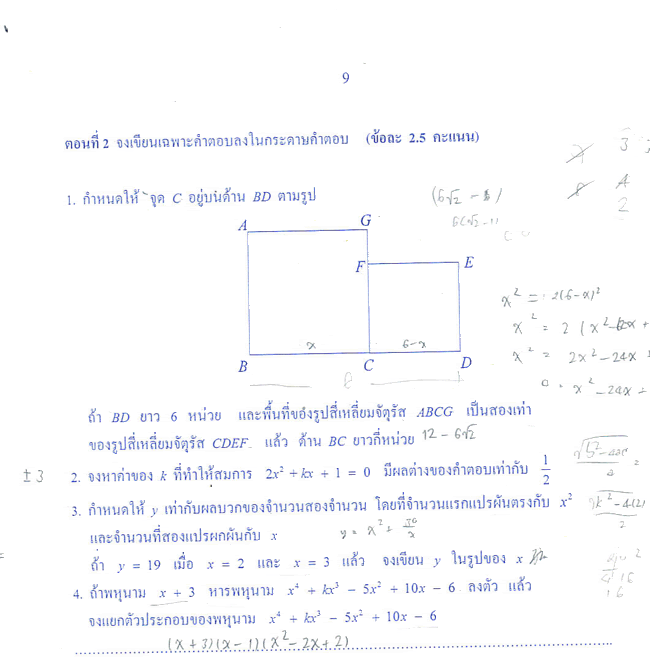   
__________________
[[:://R-Tummykung de Lamar\\::]] || (a,b,c > 0,a+b+c=3) $$\sqrt a+\sqrt b+\sqrt c\geq ab+ac+bc$$ |
|
#3
|
|||
|
|||
    ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| ที่ผิดสะเพร่า (แบบโง่ๆ) ก็มี ข้อ 2.ตอนที่ 1 .... -2 < -3 ได้ไงไม่รู้ ข้อ 8 ตอนที่ 2 ....รู้สึกว่าผมมั่วเหลือเกินำว่า เพิ่มอีกกับคำว่าเพิ่มเป็น ข้อที่ 13 ตอนที่ 2 ...pi/pi ของผมเหลือ pi อีกอะ -*- แล้วก็ออภัยหากผมทดเลอะไปหน่อยนะครับ แล้วก็ขออภัยที่มีอัพช้า เพราะว่าไปเที่ยวอยู่ครับ  ปล.ใครมีแนวคิดอะไร โพสต์มาได้เลยครับ 
__________________
[[:://R-Tummykung de Lamar\\::]] || (a,b,c > 0,a+b+c=3) $$\sqrt a+\sqrt b+\sqrt c\geq ab+ac+bc$$ |
|
#4
|
||||
|
||||
|
รูปชัดมากเลยครับ ทันใจจริง ๆ
 |
|
#5
|
||||
|
||||
|
เช่นเดียวกับกระทู้ของม.ปลาย อย่าเชื่อจนกว่าจะคิดได้ด้วยตนเอง สงสัยหรืออยากดูวิธีทำข้อใด บอกได้ครับ
ตอนที่ 1 1. ก 2. ข 3. ข. 4. ข 5. ง. 6. ง. 7. ข. 8. ข. 9. ข. 10. ข 11. ก 12. ข. 13. ข. 14. ข. 15. ก. ตอนที่ 2 1. \(BC=12-6\sqrt{2}\) 2. k=ฑ3 3. y=x2+30/x 4. \((x-3)(x-1)(x^2-2x+2)\) 5. ชนิดแรก 38kg ชนิดที่สอง 12kg 6. 108สิบสอง 7. 1เจ็ด, 23เจ็ด 8. 1.5cm 9. Sum=5+(-7)=-2 10. l(k+1) 11. (x,y)=(70,24) 12. 25% 13. 28cm 14. 3.75cm 15. 2311 16. 113, 127 17. 2n+2 18. (1) (0,-4),(4,-4),(0,-8) (2) (-2,-2),(-6,-2),(-2,-6) 19. x'=x-5, y'=y+3, d=34 20. รูปสุดท้ายได้จากหมุนจุดยอดแต่ละจุดตามเข็มนาฬิกาไป 180° 21. 2/5 22. 87 23. 17760 24. 1/3 25. ให้หลานมี n คน หลานคนสุดท้าย(คนที่ n)ได้เงิน 1000n บาท คนที่ n-1 ได้เงิน (n-1)1000+(1/9)1000n บาท สองคนนี้ได้เงินเท่ากัน ดังนั้น n=9 (หากแก้แบบนี้จะไม่เห็น trivial solution n=1 แต่ไม่น่าจะเสียหายเพราะคนที่ 0 ไม่นิยาม) edit1: แก้ข้อ 2.18.(1), 2.25
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. 04 ธันวาคม 2005 22:40 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ nongtum |
|
#6
|
|||
|
|||
|
ข้อสุดท้าย ผมแก้สมการได้ n = 1,9 ครับ
ไม่ทราบว่าเพื่อนๆมีความเห็นอย่างไรครับ (แต่ผมตอบ 9 อย่างเดียว) เนื่องจากมีคนเดียว มันไม่รู้จะเปรียบเทียบกับอะไร แต่โจทย์บอกว่า ...ทุกคน ได้เงินเท่ากัน  ----- แล้วก็ข้อ เทสซาเลชัน ผมได้ (0,-4),(0,-8),(4,-4) ครับ 
__________________
[[:://R-Tummykung de Lamar\\::]] || (a,b,c > 0,a+b+c=3) $$\sqrt a+\sqrt b+\sqrt c\geq ab+ac+bc$$ 30 พฤศจิกายน 2005 20:47 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ R-Tummykung de Lamar |
|
#7
|
||||
|
||||
|
ลองคิดดูแล้ว เห็นด้วยกับน้อง Tummy ทั้งสองข้อที่ว่ามาครับ.
 อ้อ. ลืมบอกนั่นไม่ได้เรียกว่า Tessellation นะครับ My Maths เล่ม 11 มีนิยามของเทสเซลเลชัน ลงพอดี 
__________________
The Lost Emic <<-- หนังสือเฉลยข้อสอบระดับประถมนานาชาติ EMIC ครั้งที่ 1 - ครั้งที่ 8 ชุดสุดท้าย หลงมา 
01 ธันวาคม 2005 18:24 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ gon |
|
#8
|
|||
|
|||
|
ช่วยแสดงวิธีทำข้อ 10 ตอนที่ 2 หน่อยครับ
|
|
#9
|
||||
|
||||
|
จัดให้ครับ
2.10 จากโจทย์จะได้ \(a_1=lb_1,\ a_3=lb_3,\ldots,a_{2547}=lb_{2547}\) และ \(l^2a_{2}=2lb_2,\ l^2a_{4}=4lb_4,\ldots,l^2a_{2548}=2548lb_{2548}\) นั่นคือ \[\frac{a_1+l^2a_2+a_3+l^2a_4+\cdots+l^2a_{2548}}{b_1+b_2+\cdots+b_{2548}}= \frac{l\sum_{i=1}^{2548}b_i+l(b_2+3b_4+\cdots+2547b_{2548})}{\sum_{i=1}^{2548}b_i} =l+lk=l(k+1)\] อ้อ ที่ว่า เทสเซลเลชัน นี่มันเขียนเป็นภาษาอังกฤษยังไงหรือครับ เดาไม่ถูก ไม่มี mymaths ในมือ 
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
|
#10
|
||||
|
||||
|
ถ้าคำตอบมีสองคำตอบแล้วตอบไปไม่ครบจะได้คะแนนมั้ยคะ
__________________
รักคณิตศาสตร์ |
|
#11
|
|||
|
|||
 ดีงับ ผมเป็นเพื่อนของalberta นะงับ ก็สอบสมาคมเหมือนกันแหละงับ ข้อที่คุณ tum โพสมาป๋ม ก็ตอบ 9 อย่างเดียวเหมือนกันอะ อิๆๆ เดางับ สมาคมปีนี้เขาจะเอาถึงกี่เปอร์เซนต์งับ ดีงับ ผมเป็นเพื่อนของalberta นะงับ ก็สอบสมาคมเหมือนกันแหละงับ ข้อที่คุณ tum โพสมาป๋ม ก็ตอบ 9 อย่างเดียวเหมือนกันอะ อิๆๆ เดางับ สมาคมปีนี้เขาจะเอาถึงกี่เปอร์เซนต์งับ ป.ล. alberta สัพเพร่าหลายข้อแย้วอิๆ ป๋มก็เหมือนกันงับ |
|
#12
|
|||
|
|||
|
ขอวิธีทำ ข้อ 2, 3, 7, 11, ตอนที่ 1 แล้วก็ ข้อ 13 ตอนที่ 2 หน่อยงับ ช่วยทำไห้ด้วยน่ะงับ - -*
__________________
ดีงับ |
|
#13
|
||||
|
||||
|
ใบ้ละกัน
1.2 แก้สมการทีละอสมการแล้วเขียนเส้นจำนวน 1.3 จาก x+2y=6xy จะได้ 2x+4y-3xy=9xy และ 4x+8y+3xy=27xy ดังนั้น... 1.7 หา BC โดยพีทากอรัสก่อน เพราะ BC ตั้งฉากกับ AB ดังนั้น... 1.11 ใช้สามเหลี่ยมคล้ายหาสูงตรงของกรวยเล็ก แล้วนำไปลบจากส่วนสูงของกรวยใหญ่ จะได้ความสูงของกรวย ที่เหลือตรงไปตรงมาครับ 2.13 หาปริมาตรทรงกลมทั้งสี่ลูกซึ่งเท่ากับปริมาตรของกรวยสองดันแรกลบด้วยกรวยอันแรก แล้วหารัศมีฐานของกรวยสองอันแรก จากนั้นใช้สามเหลี่ยมคล้ายหารัศมีกรวยที่ฐาน
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
|
#14
|
|||
|
|||
|
ทำไมข้อ 7 ตอนที่1 ไม่ตอบ h กำลัง2 ส่วน 2รูท2 อ่ะ ข้อ ค. อ้ะ
__________________
ดีงับ |
|
#15
|
||||
|
||||
|
1.7 $\bigtriangleup{ABC}=\frac12\cdot h\sqrt2 \cdot h=\frac{h^2}{\sqrt2}$
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
  |
 หัวข้อคล้ายคลึงกัน
หัวข้อคล้ายคลึงกัน
|
||||
| หัวข้อ | ผู้ตั้งหัวข้อ | ห้อง | คำตอบ | ข้อความล่าสุด |
| ข้อสอบสมาคม ม.ปลายปี 2548 | prachya | ข้อสอบในโรงเรียน ม.ปลาย | 32 | 30 ตุลาคม 2010 12:58 |
| ขอถามสสวท.2548หน่อยไม่มั่นใจ | Wind | ข้อสอบในโรงเรียน ประถมปลาย | 3 | 27 สิงหาคม 2007 20:37 |
| โอลิมปิกคณิตศาสตร์ 2548 รอบที่ 1 | devilzoa | ข้อสอบโอลิมปิก | 2 | 20 ธันวาคม 2005 14:21 |
| โจทย์ปัญหาคณิตศาสตร์ สวัสดีปีใหม่ 2548 ครับ | nooonuii | ปัญหาคณิตศาสตร์ทั่วไป | 71 | 08 มกราคม 2005 23:16 |
| สสวท .เริ่มรับสมัครสอบ แข่งโอลิมปิกปี 2548 | gon | ข่าวคราวแวดวง ม.ปลาย | 3 | 29 พฤษภาคม 2004 20:40 |
|
|