
 |
|
|||||||
| สมัครสมาชิก | คู่มือการใช้ | รายชื่อสมาชิก | ปฏิทิน | ข้อความวันนี้ | ค้นหา |
  |
|
|
เครื่องมือของหัวข้อ | ค้นหาในหัวข้อนี้ |
|
#1
|
||||
|
||||
|
กำหนดให้ $\gamma$ เป็นเส้นโค้งเรียบใน C และ $z$ เป็นจุดใน C ซึ่งไม่อยู่ $\gamma$ นิยาม
$$I(z)=\int_{\gamma} \frac{d\xi}{\xi-z}$$ จงพิสูจน์ว่า $I(z)$ เป็นฟังก์ชันต่อเนื่องที่ $z$ อีกข้อ.. 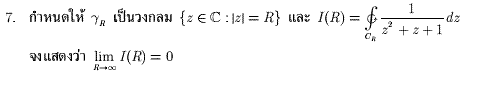
__________________
โลกนี้มีคนอยู่ 10 ประเภท คือ คนที่เข้าใจเลขฐานสอง และคนที่ไม่เข้าใจ 
18 ตุลาคม 2006 21:07 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ Mastermander |
|
#2
|
|||
|
|||
|
ผมว่าข้อล่าง โจทย์ผิดนะครับ เพราะสำหรับวงกลมที่ cover ทั้ง 2 singular points ของ integrand แล้วใช้ Cauchy residue's theorem ลิมิตต้องเข้าสู่ค่าๆหนึ่งที่ไม่เป็น 0 แน่นอน สำหรับข้อนี้
__________________
เกษียณตัวเอง ปลายมิถุนายน 2557 แต่จะกลับมาเป็นครั้งคราว |
|
#3
|
|||
|
|||
|
Solution to the second problem :
--------------------------------------------------------------------------------------------------------------- Lemma : If $f(z)=\frac{P(z)}{Q(z)}$ is a nonzero rational function with $deg(P(z))+2\leq deg(Q(z))$ then $\displaystyle{ \lim_{R\rightarrow \infty}I(R) = \lim_{R\rightarrow \infty} \int_{|z|=R} f(z) dz = 0.}$ Proof : Let $deg(P(z))=m, deg(Q(z)) = n$ and $a_m,b_n$ be leading coefficients of $P(z)$ and $Q(z)$ respectively. Then $m+2\leq n$. Note that $\displaystyle{\lim_{z\rightarrow\infty}\frac{P(z)}{a_m z^m}=\lim_{z\rightarrow\infty}\frac{Q(z)}{b_n z^n}=1.}$ Thus there is an $R>0$,sufficiently large, such that $|P(z)| < \frac{3}{2}|a_m|| z|^m$ and $|Q(z)| > \frac{1}{2}|b_n|| z|^n$ for all $|z|\geq R.$ Hence $\displaystyle{|I(R)| \leq \int_{0}^{2\pi} |f(Re^{it})(iRe^{it})|dt\leq \frac{2\pi K}{R^{n-m-1}}, K = \frac{3|a_m|}{|b_n|}. }$ Letting $R\rightarrow\infty$, we get the result. --------------------------------------------------------------------------------------------------------------- Applying this lemma to the function $\frac{1}{1+z+z^2}$, we are done. 
__________________
site:mathcenter.net คำค้น 19 ตุลาคม 2006 12:47 : ข้อความนี้ถูกแก้ไขแล้ว 4 ครั้ง, ครั้งล่าสุดโดยคุณ nooonuii |
|
#4
|
|||
|
|||
|
ขอบคุณ คุณ nooonuii สำหรับ general form ครับ
เมื่อกี้ มา check ถึงรู้ว่า ผมบวกเลขผิดนี่เอง ทีหลังจะไม่บวกเลขตอนตี 2 อีกแล้ว  จริงๆข้อนี้ ถ้าให้วงกลม รัศมี r สามารถ cover ทั้ง 2 singular points ได้ ก็จะทำให้ I(r)=0 โดยผลของ residue theorem ดังนั้นไม่ต้องสงสัยเลยว่า วงที่ใหญ่กว่านี้ทุกวง ก็ยังคงทำให้ I(R)=0 ส่วนข้อ 1 ผมว่าใช้ result ข้างล่างนี้ก็ไม่ยากที่จะพิสูจน์ว่า $ I(z) $ ต่อเนื่องที่ z= a ที่ไม่อยู่บน $ \gamma$ แล้วนะครับ $$ \mid I(z)- I(a) \mid =\mid z-a \mid \bigg | \int_{\gamma} \frac{d\xi}{(\xi-z)(\xi-a)} \bigg | $$
__________________
เกษียณตัวเอง ปลายมิถุนายน 2557 แต่จะกลับมาเป็นครั้งคราว |
|
#5
|
||||
|
||||
|
ขอบคุณครับ
__________________
โลกนี้มีคนอยู่ 10 ประเภท คือ คนที่เข้าใจเลขฐานสอง และคนที่ไม่เข้าใจ 
|
|
#6
|
||||
|
||||
|
Calculate $\int_0^\infty \frac{\sin t}{t}\ dt$ with Laplace transform ?
$$L\{\sin t\}=\frac{1}{s^2+1}\quad ,s>0$$ $$L\bigg\{ \frac{\sin t}{t}\bigg\}=\int_s^\infty \frac{dr}{1+r^2}=\frac{\pi}{2}-\arctan s$$ Can we use $s=0$ in this case ? Coz answer is correct
__________________
โลกนี้มีคนอยู่ 10 ประเภท คือ คนที่เข้าใจเลขฐานสอง และคนที่ไม่เข้าใจ 
|
|
#7
|
||||
|
||||
|
วิธีของคุณ mastermander ใช้ได้ครับไม่ผิดแต่อย่างใด
__________________
PaTa PatA pAtA Pon! |
  |
 หัวข้อคล้ายคลึงกัน
หัวข้อคล้ายคลึงกัน
|
||||
| หัวข้อ | ผู้ตั้งหัวข้อ | ห้อง | คำตอบ | ข้อความล่าสุด |
| Function problems | Far | ปัญหาคณิตศาสตร์ทั่วไป | 4 | 23 กรกฎาคม 2009 05:09 |
| อยากทราบเรื่องthree famous problems of antiquity | nongteam | ปัญหาคณิตศาสตร์ทั่วไป | 1 | 03 กันยายน 2006 04:41 |
| complex integral ครับ | Counter Striker | ปัญหาคณิตศาสตร์ทั่วไป | 2 | 19 เมษายน 2005 15:27 |
| โจทย์ complex number | brother | ปัญหาคณิตศาสตร์ทั่วไป | 3 | 19 เมษายน 2005 10:50 |
| Challenging Problems from a Book | aaaa | ปัญหาคณิตศาสตร์ทั่วไป | 19 | 23 กุมภาพันธ์ 2005 22:25 |
|
|