ข้อสอบ IMO 2004

[nithi_rung]

วันแรก

[nithi_rung]

วันที่สอง

[gon]

ขอลองข้อที่ 2 วันแรกก่อนแล้วกัน

จงหาพหุนาม P(x) ทั้งหมดซึ่งมีสัมประสิทธิ์เป็นจำนวนจริง และ สอดคล้องกับสมการ
P(a - b) + P(b - c) + P(c - a) = 2P(a + b + c) ... (*)
สำหรับทุกจำนวนจริง a, b, c ซึ่ง ab + bc + ca = 0

---

ขั้นที่ 1 : จะแสดงว่า P(0) = 0 ดังนี้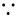
0ท0 + 0ท0 + 0ท0 = 0 ฎ แทน a = b = c = 0 ลงไปใน (*) จะได้ว่า
P(0) + P(0) + P(0) = 2P(0 + 0 + 0) ฎ P(0) = 0

ขั้นที่ 2 : จะแสดงว่า P(x) เป็นฟังก์ชันคู่ ดังนี้
ให้ a = x, b = c = 0 จะได้ว่า
P(x - 0) + P(0 - 0) + P(0 - x) = 2P(x + 0 + 0) ฎ P(-x) = P(x)

ขั้นที่ 3 : จะแสดงว่า P(x) = a₂x² + a₄x⁴ + ... + a_2mx^2m ดังนี้
สมมติให้ P(x) = a₀ + a₁x + a₂x² + a₃x³ + ... + a_nxⁿ ... (1)
\ P(-x) = a₀ - a₁x + a₂x² - a₃x³ + ... + a_n(-x)ⁿ ... (2)
เทียบสัมประสิทธิ์ของ x กำลังใด ๆ ระหว่าง (1) กับ (2) จะได้ว่า a₁ = a₃ = a₅ = ... = 0
\ P(x) = a₀ + a₂x₂ + a₄x⁴ + ... + a_2mx^2m สำหรับจำนวนเต็มบวก m ใด ๆ
แต่ P(0) = 0 ฎ a₀ = 0 ฎ P(x) = a₂x₂ + a₄x⁴ + ... + a_2mx^2m = S_{i = 1}^ma_2ix²ⁱ

ขั้นที่ 4 : จะแสดงว่า m ฃ 2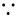
(6x)(3x) + (3x)(-2x) + (-2x)(6x) = 0 ฎ P(3x) + P(5x) + P(8x) = 2P(7x) ... [ Note P(-8x) = P(8x) ]
เทียบสัมประสิทธิ์ของ x²ⁱ ใด ๆ จาก P(x) ในขั้นที่ 3 จะได้ว่า 3²ⁱ + 5²ⁱ + 8²ⁱ = 2(7²ⁱ) หรือ 9ⁱ + 25ⁱ + 64ⁱ = 2(49ⁱ)
เมื่อ i = 1 จะได้ว่า 9ⁱ + 25ⁱ + 64ⁱ = 9 + 25 + 64 = 98
และ 2(49ⁱ) = 2(49) = 98
เมื่อ i = 2 จะได้ว่า 9ⁱ + 25ⁱ + 64ⁱ = 81 + 625 + 4096 = 4802
และ 2(49ⁱ) = 2(49)² = 4802

เมื่อ i ณ 3 จะพิสูจน์ว่า 9ⁱ + 25ⁱ + 64ⁱ > 2(49ⁱ) ดังนี้
ให้ P(n) แทนข้อความ 64ⁿ > 2(49ⁿ) ทุกจำนวนนับ n ณ 3
ขั้นฐาน : P(3) = 64³ = 262,144 > 2(49)³ = 235,298
ขั้นอุปนัย : สมมติให้ 64^k > 2(49^k) ทุกจำนวนนับ k จะแสดงว่า P(k + 1) เป็นจริง ดังนี้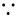
ถ้า 64^k > 2(49^k) แล้ว 64(64)^k > 64(2)(49^k) = 128(49^k) > 98(49^k) = 2(49)(49^k)
นั่นคือ 64^{k + 1} > 2(49)^{k + 1} \ P(k + 1) เป็นจริง
โดยอุปนัยเชิงคณิตศาสตร์ จึงสรุปได้ว่า P(n) เป็นจริง ทุกจำนวนนับ n ณ 3
\ 64ⁱ > 2(49ⁱ) ฎ 9ⁱ + 25ⁱ + 64ⁱ > 2(49ⁱ)
\ P(x) = a₂x² + a₄x⁴ หรือ P(x) = dx² + ex⁴ สำหรับ d, e ฮ R ใด ๆ

ขั้นที่ 5 : ตรวจสอบว่า P(x) = dx² + ex⁴ สอดคล้องตามเงื่อนไขโจทย์

เรารู้ว่า ถ้า x + y + z = 0 แล้วจะได้ว่า
1) x² + y² + z² = -2(xy + yx + zx)
2) x⁴ + y⁴ + z⁴ = 2(xy + yz + zx)²
(Note : พิสูจน์เอาเอง ขี้เกียจพิมพ์แล้ว , พิสูจน์ได้อย่างน้อย 2 วิธี คือ
ก. ถ้าสมการ x³ + px² + qx + r = 0 มีรากของสมการเป็น a, b, c แล้วจะได้ว่า S_n + pS_{n - 1} + qS_{n - 2} + rS_{n - 3} = 0 เมื่อ S_n = aⁿ + bⁿ + cⁿ , n เป็นจำนวนเต็มใด ๆ
ข. ให้ (1 + ax)(1 + bx)(1 + cx) = 1 + px + qx² + rx³ จากนั้นจึง Take log แล้วใช้ log(1 + x) = x - x²/2 + x³/3 - ... แล้วจึงเทียบสัมประสิทธิ์ของ x², x⁴ )

\ (a - b)² + (b - c)² + (c - a)² = -2[ (a - b)(b - c) + (b - c)(c - a) + (c - a)(a - b) ]
= ... กระจายแล้วจัดรูปจะได้ -2[ (ab + bc + ca) - (a² + b² + c²) ]
= 2(a² + b² + c²) = 2(a + b + c)²
[ เพราะ (a + b + c)² = a² + b² + c² + 2(ab + bc + ca) = a² + b² + c² ]

และ (a - b)⁴ + (b - c)⁴ + (c - a)⁴ = 2[ (a - b)(b - c) + (b - c)(c - a) + (c - a)(a - b) ]²
= 2(a² + b² + c²)² = 2(a + b + c)⁴

\ จาก (*) และ P(x) = dx² + ex⁴ จะได้ว่า
L.H.S. : P(a - b) + P(b - c) + P(c - a)
= d[ (a - b)² + (b - c)² + (c - a)²] + e[ (a - b)⁴ + (b - c)⁴ + (c - a)⁴]
= 2(a + b + c)² + 2(a + b + c)⁴

R.H.S : 2P(a + b + c) = 2d(a + b + c)² + 2e(a + b + c)⁴
\ L.H.S = R.S.H จึงได้ว่า P(x) = dx² + ex⁴ เป็นฟังก์ชันที่ต้องการ

[gon]

ต่อด้วย ข้อที่ 4 วันที่สอง
กำหนดจำนวนเต็ม n ณ 3 และให้ t₁ , t₂, ... , t_n เป็นจำนวนจริงบวกที่ทำให้
n² + 1 > (t₁ + t₂ + ... + t_n)(1/t₁ + 1/t₂ + ... + 1/t_n)
จงแสดงว่า t_i, t_j, t_k เป็นความยาวด้านของสามเหลี่ยมรูปหนึ่งเสมอ ทุก i, j, k ซึ่ง 1 ฃ i < j <k ฃ n

---

วิธีทำ
ต้องการพิสูจน์ว่า t_i + t_j > t_k ทุก 1 ฃ i < j <k ฃ n จะพิสูจน์โดยการหาข้อขัดแย้ง

ขั้นที่ 1 : พิจารณาผลคูณของ (t₁ + t₂ + ... + t_n)(1/t₁ + 1/t₂ + ... + 1/t_n) ซึ่งเมื่อกระจายออกมา จะมีการคูณกันทั้งสิ้น n² ครั้ง และ ได้เป็น n + S _{1 ฃi < j ฃn}(t_i/t_j + t_j/t_i) ตามเงื่อนไขโจทย์แสดงว่า n + S(t_i/t_j + t_j/t_i) < n² + 1 หรือ S(t_i/t_j + t_j/t_i) < n² - n + 1 ... (*)
ซึ่งจะมีจำนวนพจน์ทั้งหมด (n² - n)/2 พจน์ (1 วงเล็บคิดเป็น 1 พจน์)
อสมการนี้จะไม่เป็นจริงเมื่อไร ? ก็เมื่อ S(t_i/t_j + t_j/t_i) ณ n² - n + 1
โดย A.M. - G.M. จะได้ว่า (t_i/t_j + t_j/t_i) ณ 2 ดังนั้นโดยปกติแล้ว S(t_i/t_j + t_j/t_i) จะมีค่าอย่างน้อยเท่ากับ n² - n แต่ถ้าเราต้องการให้มันมีค่าอย่างน้อยเป็น n² - n + 1 จะต้องหมายความว่าอะไรได้บ้าง ?

สมมติว่าเราแบ่ง S(t_i/t_j + t_j/t_i) ออกเป็น 2 กลุ่มใหญ่ กลุ่มที่หนึ่งมี m พจน์ กลุ่มที่สอง ก็จะมี (n² - n)/2 - m สมมติให้คิดว่าแต่ละพจน์ในกลุ่มที่สอง มีค่าอย่างน้อยคือ 2 เท่าเดิม ดังนั้นผลบวกในกลุ่มที่สองจะมีค่าอย่างน้อยเท่ากับ 2[ (n² - n)/2 - m ] = n² - n - 2m
\ ถ้าเราอยากให้ผลบวกของทั้งหมดมีค่าอย่างน้อย n² - n + 1 แสดงว่าผลบวกของจำนวนทั้งหมด m พจน์ในกลุ่มที่หนึ่งจะต้องมีค่าอย่างน้อย 2m + 1 เพราะ (n² - n + 1) - (n² - n - 2m) = 2m + 1


ขั้นที่ 2 : สมมติให้ t_i + t_j ฃ t_k ต้องการจะพิสูจน์ข้อความดังกล่าวเป็นไปไม่ได้ ดังนี้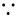
t_i + t_j ฃ t_k ฎ (t_i/t_k) + (t_j/t_k) ฃ 1 ... (1)
ถ้าเราบวกส่วนกลับของแต่ละตัวใน ด้านซ้ายมือของ (1) จะได้ครบคู่ คือเป็น (t_i/t_k + t_k/t_i) + (t_j/t_k + t_k/t_j) ซึ่งอยู่ในรูปแบบของS(t_i/t_j + t_j/t_i) โดยมี 2 พจน์ หรือ m = 2 (ซึ่งคือจำนวนกลุ่มของกลุ่มที่หนึ่ง ในขั้นที่ 1) และ จะได้ว่า 2m + 1 = 2(2) + 1 = 5

สมมติให้ a = t_i/t_k และ b = t_j/t_k จาก (1) ก็จะได้ว่า a + b ฃ 1 ... (2)
\ (t_i/t_k + t_k/t_i) + (t_j/t_k + t_k/t_j) = (a + 1/a) + (b + 1/b)
\ การพิสูจน์ว่า t_i + t_j ฃ t_k ;ว่าเป็นไปไม่ได้ ก็คือการพิสูจน์ว่า (a + 1/a) + (b + 1/b) ณ 5 เมื่อ a + b ฃ 1 นั่นเอง

ขั้นที่ 3 : พิสูจน์ว่า (a + 1/a) + (b + 1/b) ณ 5 เมื่อ a + b ฃ 1
a + 1/a = (a² + 1)/a = [ (a² - a + 1/4) + a + 3/4 ] /a
= [ (a - 1/2)² + a + 3/4 ] /a ณ (a + 3/4)/a = 1 + 3/(4a)
\ b + 1/b ณ 1 + 3/(4b)
ฎ (a + 1/a) + (b + 1/b) ณ 2 + (3/4)(1/a + 1/b) = 2 + (3/4)(4) = 5 จบ.
(เพราะ จากอสมการ A.M. ณ H.M. จะได้ว่า (a + b)/2 ณ 2/(1/a + 1/b) แต่จาก (2) จะได้ว่า (a + b)/2 ฃ 1/2 \ 2/(1/a + 1/b) ฃ 1/2 ฎ 1/a + 1/b ณ 4)

ข้อความเดิมของคุณ nithi_rung:
วันที่สอง