
 |
|
|||||||
| สมัครสมาชิก | คู่มือการใช้ | รายชื่อสมาชิก | ปฏิทิน | ข้อความวันนี้ | ค้นหา |
  |
|
|
เครื่องมือของหัวข้อ | ค้นหาในหัวข้อนี้ |
|
#1
|
|||
|
|||
|
มีเรื่องอยากจะให้ทุกๆ คนช่วยกันหาคำตอบหน่อยครับ
ปัญหาที่ 1 :  พื้นที่ผิวของทรงกลมมีความสัมพันธ์กับปริมาตรของทรงกลมอย่างไร? ปัญหาที่ 2 :  อยากทราบที่มาของสูตรพื้นที่ผิวของทรงกลม 4pr2 และอยากทราบที่มาของสูตรปริมาตรของทรงกลม 4/3pr3 หมายความว่า เขาใช้วิธีใดถึงคิดออกมาได้ว่า การหาพื้นที่ผิวและปริมาตรของทรงกลมจึงใช้สูตรนี้ พรุ่งนี้จะมาติดตามคำตอบนะครับ... 
__________________
ความรู้ทางคณิตศาสตร์มีค่าเป็นอสงไขย มิใช่สงไขยที่มีความจำกัด |
|
#2
|
||||
|
||||
|
ขอลองอธิบายเองบ้าง ยืนดีรับฟังคำถามและข้อเสนอแนะเพิ่มเติมครับ
 1. หาได้โดยหาอัตราส่วนหรือแทนค่าหลายๆค่าแล้วคำนวณหาอัตราส่วนครับ 2. เราอาจมองง่ายๆ(อ้างจากที่นี่ หากสงสัยที่มาของสูตรอื่นลองคลิกด้านล่างของหน้านั้น หรือไม่ลองกูเกิลดูครับ)ได้ดังนี้ สำหรับพื้นที่ผิวทรงกลม(รัศมี r): ตอนแรกให้เอาทรงกระบอกรัศมีฐาน r สูง 2r มาครอบ แล้วชอยทรงกระบอกตามขวางเป็นแผ่น'บางๆ'หลายๆแผ่น ซึ่งจะได้ว่าพื้นที่ผิวด้านข้างของแผ่นทรงกระบอกแต่ละชิ้นมีค่าใกล้เคียงกับพื้นที่ผิวทรงกลมที่ถูกตัดออกมา นั่นคือ พื้นที่ผิวของทรงกระบอกเท่ากับพื้นที่ผิวทรงกลมคือ 2pr x 2r=4pr2 ปริมาตรทรงกลม(รัศมี r): เนื่องจากเราสามารถแบ่งทรงกลมออกเป็นพีระมิดฐานโค้งเล็กๆหลายๆอันที่มีจุดยอดเป็นจุดศูนย์กลางของทรงกลมและมีพื้นที่ฐานเป็นส่วนหนึ่งขอ งทรงกลม เมื่อเราซอยพีระมิดเหล่านี้'เล็ก'พอ เราสามารถประมาณฐานโค้งๆนี้เป็นฐานเรียบๆได้ ส่วนสูงของพีระมิดย่อยนี้มีค่า(ประมาณ)เป็น r ดังนั้น ปริมาตร =ผลรวมปริมาตรพีระมิดย่อย=(1/3)p(พื้นที่ผิวทรงกลม)r=(4/3)pr3 กระบวนการดังกล่าวมี error จากการประมาณเสมอ (ซึ่งเกี่ยวข้องกับการที่ p เป็นจำนวนอตรรกยะ) ในคณิตศาสตร์ระดับสูงเราสามารถพิสูจน์สูตรเหล่านี้โดยแคลคูลัสครับ เช่น ปริมาตรทรงกลม $V(r)=\int_0^r 4\pi r^2\ dr$ เป็นต้นครับ
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. 16 มีนาคม 2006 20:24 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ nongtum |
|
#3
|
|||
|
|||
|
ขอบคุณครับที่ให้คำแนะนำดีๆ แต่ว่าพอลองไปเปิดในเว็บที่แนะนำมา
 แปลไม่ออกเลยครับ แปลไม่ออกเลยครับ  นี่มีข้อความที่ลอง search หาดู ปรากฏว่าไปเจอเรื่องราวเกี่ยวกับปริมาตรทรงกลม ดังนี้ครับ นี่มีข้อความที่ลอง search หาดู ปรากฏว่าไปเจอเรื่องราวเกี่ยวกับปริมาตรทรงกลม ดังนี้ครับThere is a classic Greek proof, which does not explicitly use calculus. [Calculus as we know it was created much later.] The secret is this: Take a hemisphere. Surround it by a cylinder of the same radius as the hemisphere, and the height of the hemisphere. We assume you know the volume of this cylinder. \((\pi R^2)(R)\) = Area of base ด height. Now, take an inverted right circular cone in the cylinder. with the 'base' of the cone at the top of the cyliner, and the point at the bottom (at the center of the hemisphere). We assume you know the volume of a cone: \( \frac{1}{3} \) ด base ด height = \( \left(\frac{1}{3}\right)(\pi R^2)(R) \) Proposition: On any horizontal slice of this configuration, the area of the cross section of the hemisphere = the area of the cross section of the cylinder - the area of the cross section of the inverted cone. Proof: This just involves writing out the areas of the three different circles and seeing that the way the radius of the circular cross section of the hemisphere changes and the way the cross section of the cone changes match up. Conclusion (General principle): If two solids have cross sections of equal area for all horizontal slices, then the have the same volume. Therefore the volume of the hemisphere = volume of cylinder - volume of cone = $ \pi R^3 - \left(\frac{1}{3}\right)\pi R^3 $ = $ \left(\frac{2}{3}\right) \pi R^3 $ The volume of the sphere is twice that = $ \mathbf{\frac{4}{3} \pi R^3} $ ถ้าใครแปลออก ช่วนแปลหรือสรุปเป็นเรื่องเป็นราวให้หน่อยครับ 
__________________
ความรู้ทางคณิตศาสตร์มีค่าเป็นอสงไขย มิใช่สงไขยที่มีความจำกัด 14 มีนาคม 2006 15:41 : ข้อความนี้ถูกแก้ไขแล้ว 2 ครั้ง, ครั้งล่าสุดโดยคุณ promath |
|
#4
|
|||
|
|||
|
ขอช่วยขยายความในเรื่องของพื้นที่ผิวของทรงกลมอีกหน่อยนะครับ คือว่ายังไม่เข้าใจ เปิดไปดูตามเว็บไซต์ต่างๆ เขาก็ใช้หลักการที่นำทรงกระบอกและกรวยมาเกี่ยวข้องด้วยครับ
http://mathcentral.uregina.ca/qq/dat...artridge1.html  http://www.qc.edu.hk/math/Junior%20Secondary/Sphere.htm 
__________________
ความรู้ทางคณิตศาสตร์มีค่าเป็นอสงไขย มิใช่สงไขยที่มีความจำกัด |
|
#5
|
||||
|
||||
|
จากลิงค์ที่ให้มา ทั้งหมดเป็นการแสดงว่าหากเอาครึ่งทรงกลม กรวยและทรงกระบอกที่มีรัศมีฐานยาว $r$ เท่ากัน กรวยและทรงกระบอกสูง $r$ เอาทรงกระบอกครอบกรวยให้ฐานกรวยอยู่ด้านบน และวางครึ่งทรงกลมให้ฐานของครึ่งทรงกลมอยู่ด้านล่าง จะได้ว่าหลังจาก'ซอย'หน้าตัดขนานกับฐานแล้ว ในแต่ละหน้าตัด
พื้นที่วงแหวนที่ได้จากทรงกระบอกกับกรวย=พื้นที่ของหน้าตัดที่เกิดจากครึ่งทรงกลม ซึ่งแสดงได้ดังนี้: ณ ความสูง $a$ จากฐานครึ่งทรงกลม มีพื้นที่หน้าตัดเป็น $\pi\sqrt{r^2-a^2}$ (รัศมีหาได้โดยทฤษฎีบทพีทากอรัส) เนื่องจากรัศมีของหน้าตัดกรวยเท่ากับความสูง $a$ เพราะหากลองผ่ากรวยจากปลายลงมาตามแกนกรวย จะเห็นว่าหน้าตัดที่ได้เป็นสามเหลี่ยมหน้าจั่วที่มีมุมที่ฐานเป็น 45° และส่วนสูง $a$ แบ่งครึ่งมุมยอดของสามเหลี่ยมหน้าจั่ว(ซึ่งเป็นมุมฉาก) พื้นที่วงแหวนจึงเป็น $\pi\sqrt{r^2-a^2}$ ### การพิสูจน์ดังกล่าวอาศัยว่า เราทราบปริมาตรของกรวยและทรงกระบอก และข้อเท็จจริงที่ว่าหากพื้นที่หน้าตัดและส่วนสูงมีขนาดเท่ากันปริมาตรจะเท่ากัน ดังนั้น ปริมาตรของครึ่งทรงกลมจึงต้องเท่ากับปริมาตรของทรงกระบอกหักออกด้วยปริมาตรกรวย ส่วนพื้นที่ผิวทรงกลม จากที่กล่าวด้านบนหากเรามองว่าในแต่ละส่วนตัด(ที่บางพอ) พื้นผิวเอียงๆด้านข้างของส่วนตัดทรงกลมและทรงกระบอกด้านข้างจะไม่แตกต่างกันมาก (นั่นคือลบกันแล้วได้ค่าใกล้ศูนย์) แต่หากใช้แคลคูลัส จะได้ว่าพื้นที่ผิวด้านข้างของครึ่งทรงกลมเป็น $R^2\int_0^{2\pi}\int_0^{\pi/2} \sin\varphi\ d\varphi d\theta=2\pi R^2$
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. 14 มีนาคม 2006 20:06 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ nongtum |
|
#6
|
|||
|
|||
|
ปัญหาที่ 3 :
$\qquad\quad $ในประเทศฝรั่งเศส นอกจากหอไอเฟล ซึ่งเป็นสถานที่ที่สำคัญแล้ว ยังมีพิพิธภัณฑ์ลูฟว์ (Louvre) ในกรุงปารีส ที่นี่เป็นที่รวบรวมงานศิลปะของศิลปินระดับโลก เช่น ภาพวาดโมนาลิซา ของลีโอนาร์โด ดาวินซี (Leonado da Vinci) $\qquad\quad $เว็บไซต์แห่งหนึ่งกล่าวถึงอาคารทางเข้าพิพิธภัณฑ์ซึ่งเป็นพีระมิดกระจกไว้ว่า พีระมิดดังกล่าวมีความสูง 21.65 เมตร วัดความยาวของฐานโดยรอบได้ 140 เมตร และมีปริมาตรประมาณ 8,840 ลูกบาศก์เมตร $\qquad\quad $นาย ก คิดว่าพีระมิดที่ว่านี้เป็นพีระมิดฐานสามเหลี่ยมด้านเท่า แต่นาย ข ไม่เห็นด้วย และคิดว่าน่าจะเป็นพีระมิดฐานสี่เหลี่ยมจัตุรัส ความคิดของใครน่าจะถูกต้อง เพราะเหตุใด   ปัญหาที่ 4 : $\qquad\quad $ถ้าตัดมุมของลูกบาศก์ทั้งแปดมุมด้วยระนาบให้ผ่านจุดกึ่งกลางขอบของลูกบาศก์ตามรอยเส้นประ ดังแสดงในรูป จะได้รูปเรขาคณิตสามมิติ 14 หน้าชนิดหนึ่ง เรียกว่า คิวบอกตะฮีดรอน (Cuboctahedron) ที่มีหน้า 6 หน้าเป็นรูปสี่เหลี่ยมจัตุรัส อีก 8 หน้าเป็นรูปสามเหลี่ยมด้านเท่า ปริมาตรของคิวบอกตะฮีดรอนเป็นกี่เท่าของลูกบาศก์เดิม (ขอแก้ไขรูปภาพหน่อยนะครับ ถ้าใครมีความคิดอะไรเพิ่มเติม ก็โพสท์ลงบอร์ดได้นะครับ อย่าลืมซ่อนคำตอบไว้ด้วยนะครับ เดี๋ยวคนอื่นเห็น อิ..อิ..  คุณ nongtum ผมคิดว่าข้อ 4 ผมมีความคิดเห็นที่ต่างออกไปนะครับ แต่ลืมเเล้วว่าคิดยังไง เดี๋ยวขอกลับไปจูนเครื่องก่อนนะครับ) คุณ nongtum ผมคิดว่าข้อ 4 ผมมีความคิดเห็นที่ต่างออกไปนะครับ แต่ลืมเเล้วว่าคิดยังไง เดี๋ยวขอกลับไปจูนเครื่องก่อนนะครับ)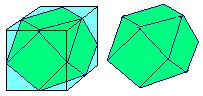
__________________
ความรู้ทางคณิตศาสตร์มีค่าเป็นอสงไขย มิใช่สงไขยที่มีความจำกัด 17 มีนาคม 2006 14:49 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ promath |
|
#7
|
||||
|
||||
|
คำถามไม่ยากครับ แต่เนื้อหาคำถามน่าสนใจดี ขอละวิธีคิดละกันนะครับ
ฐานเป็นสี่เหลี่ยมจัตุรัส (อย่าปล่อยให้รูปหลอกตา) 5/6 (แก้ไขคำตอบข้อ 4)
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. 19 มีนาคม 2006 19:30 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ nongtum |
|
#8
|
|||
|
|||
|
สำหรับแนวความคิดปัญหาที่ 4 ของผมและเพื่อนๆ ที่ไปช่วยกันคิดมีดังนี้ครับ (ไม่รู้ว่าถูกป่าว)
$\qquad\qquad$จากรูปลูกบาศก์กำหนดให้แต่ละด้านยาว $a$ หน่วย ดังนั้น ปริมาตรของลูกบาศก์เท่ากับ $a^3$ (พักไว้ก่อนนะ) $\qquad\qquad$จะเห็นได้ว่ามุมทั้ง 8 มุมของลูกบาศก์ถูกตัดออกไปเป็นรูปพีระมิด (ไม่แน่ใจว่ารูปชัดเจนหรือเปล่า) ดังนั้น ปริมาตรของพีระมิดทั้ง 8 รูป เท่ากับ $\displaystyle{8\times\left[\frac{1}{3}\times\left(\frac{1}{2}\times\frac{a}{2}\times\frac{a}{2}\right)\times\frac{a}{2}\right]}\;=\;\frac{a^3}{6}$ เมื่อ $\displaystyle{\frac{a}{2}}$ เป็นความยาวของฐานแต่ละด้านที่ถูกแบ่งครึ่งออกจากแต่ละด้านของลูกบาศก์ และ $\displaystyle{\frac{1}{2}\times\frac{a}{2}\times\frac{a}{2}}$ เป็นพื้นที่ของรูปสามเหลี่ยม $\displaystyle{\left(\frac{1}{2}\timesฐาน\timesสูง\right)}$ $\qquad\qquad$ดังนั้น ปริมาตรของคิวบอกตะฮีดรอน = ปริมาตรของลูกบาศก์ - ปริมาตรของพีระมิดทั้ง 8 รูป $$ \begin{array}{rcl}a^3 - \frac{a^3}{6} & = & \frac{6a^3 - a^3}{6} \\ & = & \frac{5}{6}a^3 \end{array}$$ $ \qquad\qquad $ นั่นคือ ปริมาตรของคิวบอกตะฮีดรอน คิดเป็น $ \displaystyle{ \frac{5}{6} } $ เท่าของปริมาตรของลูกบาศก์เดิม $\qquad\qquad $ถ้าความคิดของเพื่อนๆ และผมนั้นผิดไป ก็ขอช่วยชี้แจงแถลงไขให้ผมเข้าใจด้วยนะครับ   
__________________
ความรู้ทางคณิตศาสตร์มีค่าเป็นอสงไขย มิใช่สงไขยที่มีความจำกัด |
|
#9
|
||||
|
||||
|
คุณ promath ตอบถูกแล้วครับ ผมนับจำนวนมุมที่ตัดผิดไปเอง ข้อนี้อาจคิดง่ายๆบรรทัดเดียวจบได้ดังนี้:
$$\text{Volume}=\text{total}-\text{cut}=1-8\cdot\frac{1}{3}\cdot(\frac{1}{2})^4=\frac{5}{6}$$
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
  |
|
|