
 |
|
|||||||
| สมัครสมาชิก | คู่มือการใช้ | รายชื่อสมาชิก | ปฏิทิน | ข้อความวันนี้ | ค้นหา |
  |
|
|
เครื่องมือของหัวข้อ | ค้นหาในหัวข้อนี้ |
|
#1
|
||||
|
||||
|
ใครรู้วิธีคิดก็ช่วยแสดงวิธีคิดให้ดูหน่อยนะครับ
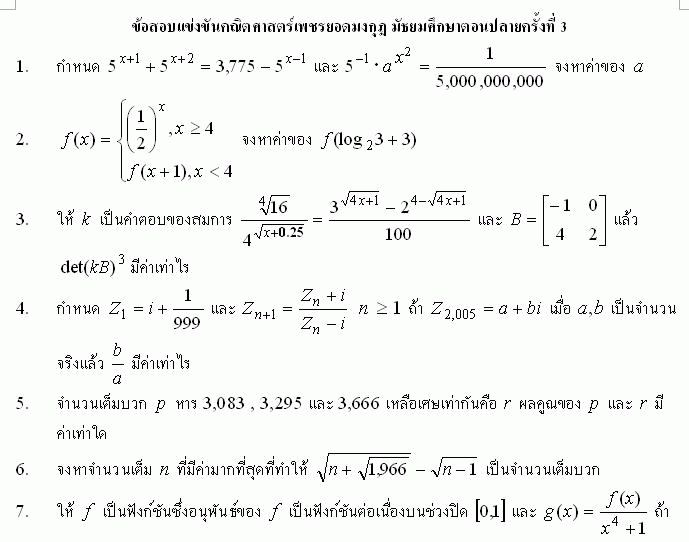 |
|
#2
|
||||
|
||||
|
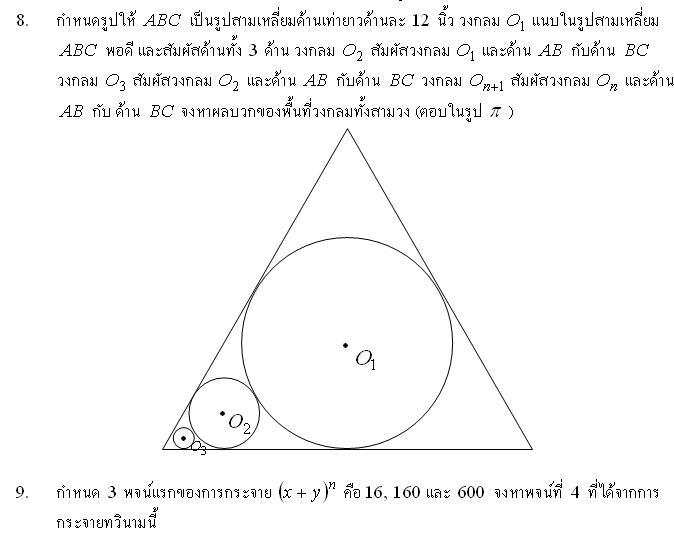
ต่อครับ
 |
|
#3
|
||||
|
||||
|
เหลืออีก 2
 |
|
#4
|
||||
|
||||
|
อีก1
 |
|
#5
|
||||
|
||||
|
อันสุดท้ายครับ ถ้าผมคิดได้แล้วผมจะมาเฉลยให้นะครับ
 |
|
#6
|
||||
|
||||
|
เท่าทีดู ยากเอาการแฮะ...
โจทย์ข้อเจ็ด ส่วนคำถามหายไปครับ ส่วนข้ออื่นยังไม่ได้คิดเลยเพราะเนตที่หอกำลังเจ๊ง TT ไว้คิดได้สักสามสี่ข้อจะมาโพสต์นะครับ
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
|
#7
|
|||
|
|||
|
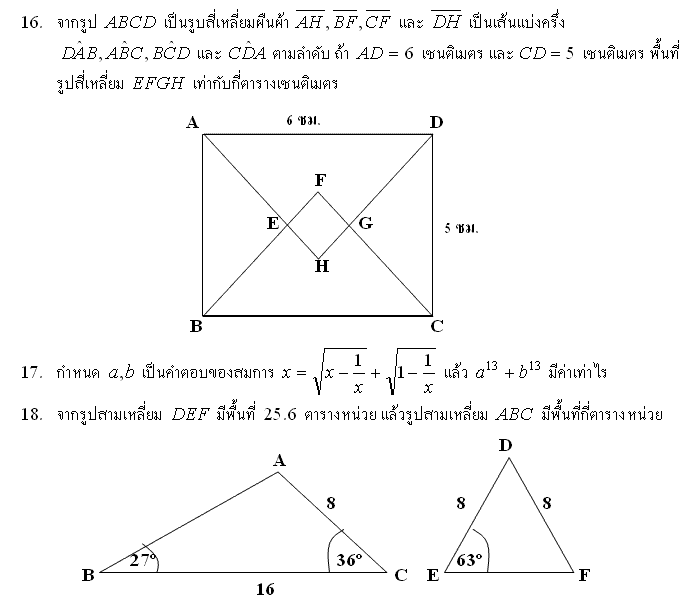
ข้อ 16
เพราะ ึ2cos(45-n)= cos(n)+sin( n) จากนั้นก็แทน n= 1,2,3,...,44 ลงไป ก็จะได้สมการ 44 สมการ ซึ่งเมื่อนำมารวมกัน จะได้ \[ \sqrt{2}\sum_{i=1}^{44}cos(i) =\sum_{i=1}^{44}cos(i) +\sum_{i=1}^{44}sin(i) \] เมื่อหารด้วย summation ของ sine จะได้ คำตอบที่ต้องการ นั่นคือ ึa +ึb= ึ2 +1 ข้อนี้จึงตอบ 3
__________________
เกษียณตัวเอง ปลายมิถุนายน 2557 แต่จะกลับมาเป็นครั้งคราว |
|
#8
|
||||
|
||||
|
1. จาก \(\displaystyle\large{30\cdot5^x=151\cdot25-\frac{5^x}{5}}\) จะได้ x=3 และจาก \(\displaystyle\large{\frac{a^{x^2}}{5}=\frac{1}{5\cdot10^9}}\) จะได้ a=0.1
2. เนื่องจาก log23>1 ดังนั้น f(3+log23)=f(log224)=1/24 3. จาก \(100(2^{1-\sqrt{4x+1}})=3^{\sqrt{4x+1}}-\frac{16}{2^{\sqrt{4x+1}}}\) จะได้ x=2=k และ det(kB)3=(4det(B))3=-512 5. gcd(3295-3083,3666-3295)=53=p, r=9, pr=477 8. เราจะได้ว่า rOn=3rOn+1 รัศมีวงกลม \(r_1=\frac{\sqrt{3}}{4}\frac{12^2}{18}=2\sqrt{3}\) และพื้นที่วงกลมทั้งสามเป็น \((1+\frac{1}{9}+\frac{1}{81})(2\sqrt{3})^2\pi=\frac{364}{27}\pi\) 9. จากโจทย์จะได้ \(x^n=16,\ nx^{n-1}y=160,\ \frac{n(n-1)}{2}x^{n-2}y^2=600\) นั่นคือ \(\frac{y}{x}=\frac{10}{n},\ \frac{n-1}{2}\frac{y}{x}=\frac{15}{2}\Rightarrow\ n=4,\ x=2,\ y=5\) ดังนั้นเทอมที่สี่ได้แก่ 1000 10. \(A=\sum(\frac{1}{4n-3}-\frac{1}{4n+1})=1\), \(B=\sum(\frac{1}{n^2}-\frac{1}{(n+1)^2})=1\) ดังนั้นคำตอบคือ 2 11. ให้ \((f+g)(x)=ax^2+bx+c\) จะได้ \(f((f+g)(x))=2ax^2+2bx+2c+1=x^2+2x+4\) หรือ a=1/2, b=1, c=3/2 g(x)=(f+g)(x)-f(x)=\(\frac{1}{2}x^2-x+\frac{1}{2}\), \((g\circ{f})(x)=g(2x+1)=2x^2,\ f^{-1}(x)=\frac{x-1}{2}\) ดังนั้นจะได้พจน์ที่โจทย์ถามคือ \((g\circ{f})(x)\cdot{f^{-1}(x)}=x^3-x^2\) 12. ให้ \(y=\frac{1-x}{1+x}\) จะได้ \(x=\frac{1-y}{1+y}\) และ \(f(y)=\frac{2y}{y^2+1}\) นั่นคือ \(f(\sqrt{2}-1)=\frac{1}{\sqrt{2}}\) ตามเงื่อนไขโจทย์จะได้ \(\theta=\frac{3\pi}{4}\) 13. \(\frac{\cos{3x}}{\cos{x}}=4\cos^2{x}-3=\frac{1}{3}\) จะได้ \(\cos^2{x}=\frac{5}{6},\ \sin^2{x}=\frac{1}{6}\) และ \(\frac{\sin{3x}}{\sin{x}}=3-4\cdot\frac{1}{6}=\frac{7}{3}\) 14. วงกลมทั้งสามมีรัศมียาวเท่ากันคือ \(r=4\sqrt{2}\) เส้นผ่านศูนย์กลางของทั้งสามวงกลม colinear และวงกลม O2, O3 สัมผัสที่จุดศูนย์กลางของวงกลม O1 ดังนั้นพื้นที่แรเงาจึงเป็น \(3\pi{r^2} -2(\frac{1}{3}\pi{r^2}+2(\frac{1}{6}\pi{r^2}-\frac{\sqrt{3}}{4}\pi{r^2})) =32(\frac{4}{3}\pi-\sqrt{3})\) 17. เราจะได้ \(\frac{5}{\log{a}}=\frac{1}{\log{b}}+\frac{1}{\log{c}}\) นั่นคือ \[\frac{\log_{b}{a}+\log_{c}{a}}{5\log_{a}{b}-\log_{c}{b}} =\frac{\log{a}}{\log{b}}\cdot\frac{5/\log{a}}{1/\log{b}}=5\] 19. \(F(x)=(fog)(x)=\sqrt{x}+1,\ F^{-1}(x)=(x-1)^2,x\ge1\Rightarrow\ F'(x)=2(x-1),\ F^{-1}(2)=2\) 21. โดย little Fermat จะได้ \(n^{13}\equiv{n}\bmod{13},n^{5}\equiv{n}\bmod{5}\) ดังนั้น \(65|\underbrace{(5n^{13}-5n)+(13n^5-13n)}_{=5n^{13}+13n^5-18n}\) ดังนั้น จาก -18+65k=9a จะได้ว่า 9 หารทางซ้ายมือลงตัวเมื่อ 9|k ดังนั้นจะได้จากโจทย์ว่า k=9 แทน k แล้วแก้สมการหา a จะได้ a=63 เป็นค่าต่ำสุด 22. \(A=\frac{z}{(z-1)^2}\) คำตอบคือ -1/3 23. (ไม่ชัวร์) \(\frac{\sum(\bar{x}-x_i)}{120}=\frac{25}{4}\) ดังนั้น SD=2.5, Mean=3000/120=25, Z(สมศรี)=(30-25)/2.5=2 ดังนั้นครูสมัยจะเกษียณในอีก 31.25 หรือ 28.75 ปี (โจทย์ไม่ได้บอกว่าใครแก่กว่า) 24. จาก \(f(a)+f(2^n-a)=n^2\) เราจะทำดังนี้ f(46)+f(2002)=121, f(18)+f(46)=36, f(14)+f(18)=25, f(14)+f(2)=16, f(2)+f(2)=4 ดังนั้น f(2)=2, f(14)=14, f(18)=11, f(46)=25, f(2002)=96 มีที่พลาดตรงไหนบอกด้วยนะครับ แล้วจะมาแก้หากได้เข้าเนต ^_^ Edit1: แก้คำผิด Edit2: ตามล้างตามเช็ดที่ผิดตามคำแนะนำด้านล่าง (ข้อสอบกินแร~~~ง) ข้อ 14 คำตอบไม่ตรงกันอีกแล้ว Edit3: แก้ข้อ 21 ตามคำท้วงจากกระทู้อื่น
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. 22 กันยายน 2005 00:38 : ข้อความนี้ถูกแก้ไขแล้ว 3 ครั้ง, ครั้งล่าสุดโดยคุณ nongtum |
|
#9
|
|||
|
|||
|
มาเก็บตกรายละเอียดของคุณ nongtum ซักเล็กน้อยนะครับ
ข้อ 3 เนื่องจาก B มีมิติ 2x2 ดังนั้น det(2B)3 = (det(2B))3=(4det(B))3 = -512 ข้อ 11 ผมว่า เขาถามตัวนี้ นะครับ \(\large ((g\circ f) \cdot f^{-1})(x) \) แต่ที่คุณ nongtum ตอบ คือ \(\large ((g\circ f) \circ f^{-1})(x) \) ข้อ 13 ในส่วนของวิธีทำ \(\large cos^{2}x=\frac{5}{6} \) ข้อ 14 ผมได้คำตอบ \(\large \frac{32\pi}{3}+64\sqrt{3} \) ยังไงก็ check อีกทีแล้วกันนะครับ ข้อ 19 ฝากเจ้าของข้อสอบมายืนยัน อีกที นะครับว่า รอย dash จางๆ เหนือ F-1 คือ diff ใช่หรือไม่ แล้วก็แถมข้อ 15 ให้ครับ จาก B= -BT ดังนั้น det(B) =0 และทำให้ det(D) =0 และ จาก A= B-C ...(1) transpose both sides AT= BT-CT=-B-C ...(2) จาก (1) และ (2) จะได้ \(\large C= \frac{-1}{2}(A+A^{T}) \) ซึ่งเมื่อคำนวณ C ออกมาแล้ว จะได้ det(C)= -12 ข้อนี้ จึงตอบ -12
__________________
เกษียณตัวเอง ปลายมิถุนายน 2557 แต่จะกลับมาเป็นครั้งคราว |
|
#10
|
||||
|
||||
|
ขอบคุณมากครับ โพสต์แค่วันเดียวก็มาตอบกันเยอะขนาดนี้แล้ว งั้นเดี๋ยวผมจะโพสต์ของ ม.ต้นต่อให้นะครับ
ส่วนอันนี้ ข้อ 7 ที่หายไปครับ 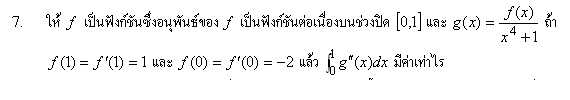 |
|
#11
|
||||
|
||||
|
อะข้อ 11 ของคุณ nongtum เข้าใจผิดนะครับ มันต้องเป็นการคูณ ฟังก์ขันครับ
รู้สึกข้อ 11 จะตอบ x3-x2 นะครับ ส่วนอันนี้ข้อสอบของ ม.ต้น ครับ ผมอยากรูวิธีคิด ข้อ 4 ของ ม.ต้น อะครับ ใครว่างก็ช่วยบอกทีนะครับ  |
|
#12
|
||||
|
||||
|
ต่อเลยนะครับ อะลืมบอกไปรู้สึกอันนี้จะเป็นของรอบชิง ม.ต้น เพชรยอดมงกุฎอะครับ
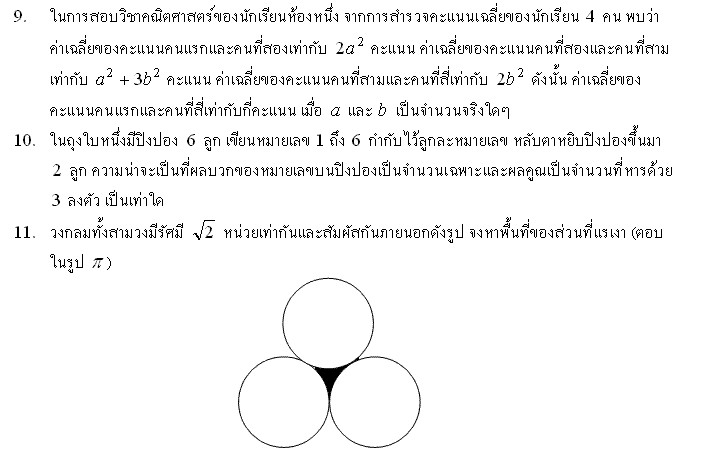 |
|
#13
|
||||
|
||||
|
ส่วนใครอยากได้ตัวข้อสอบที่ผมพิมพ์ทั้งชุดก็บอกได้นะครับ เดี๋ยวผมจะโพสต์ลิงค์ให้โหลดกัน
 |
|
#14
|
||||
|
||||
|
ต่อเลยนะครับ
 |
|
#15
|
||||
|
||||
|
ขอบคุณมากนะครับสำหรับคนที่ช่วยตอบให้
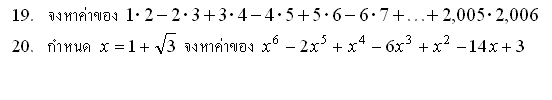 |
  |
|
|