
 |
|
|||||||
| สมัครสมาชิก | คู่มือการใช้ | รายชื่อสมาชิก | ปฏิทิน | ข้อความวันนี้ | ค้นหา |
  |
|
|
เครื่องมือของหัวข้อ | ค้นหาในหัวข้อนี้ |
|
#1
|
||||
|
||||
|
ขอความกรุณาเพื่อนๆ หรือพี่ๆ ที่มีความรู้เรื่องฟังก์ชันคอมโพสิท ช่วยแนะนำวิธีการหาโดเมนและเรนจ์ของฟังก์ชันคอมโพสิทที่ถูกต้องตามหลักการทางคณิตศาสตร์ให้ผมด้วยครับ เพราะตอนนี้ผมเกิดความสับสนมากๆ ครับว่า วิธีการหาโดเมนและเรนจ์ของฟังก์ชันคอมโพสิทนั้น ควรดำเนินการตามขั้นตอนอย่างไรกันแน่ ขอความกรุณาอธิบายแนวคิดให้ผมทราบเป็นขั้นตอนด้วยนะครับ
ช่วยอธิบายวิธีทำจากโจทย์ต่อไปนี้ จะขอบคุณมากๆเลยครับ ผมจะได้นำไปเป็นแนวทางในการทำโจทย์ข้ออื่นๆ ต่อไป  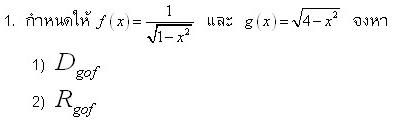 15 กุมภาพันธ์ 2006 02:35 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ Eddie |
|
#2
|
|||
|
|||
|
จะเห็นว่า $D_f=[-1,1]$ และ $D_g=[-2,2]$
เรารู้ว่า range ของ $\sqrt{1-x^2}$ คือ $[0,1]$ ดังนั้น range ของส่วนกลับของ $\sqrt{1-x^2}$ ซึ่งก็คือ $R_f$ จึงมีค่าเท่ากับ $[1,\infty)$ เนื่องจาก $$D_{g\circ f}=\{x\in D_f\mid f(x)\in R_f\cap D_g=[1,2]\}$$ เราจึงหาได้ว่า $D_{g\circ f}=[-\sqrt 3/2,\sqrt 3/2]$ และเนื่องจาก $$R_{g\circ f}=\{g(x)\mid x\in\ R_f\cap D_g=[1,2]\}$$ เราจึงหาได้ว่า $R_{g\circ f}=[0,\sqrt3]$ ครับ  15 กุมภาพันธ์ 2006 17:22 : ข้อความนี้ถูกแก้ไขแล้ว 3 ครั้ง, ครั้งล่าสุดโดยคุณ warut |
|
#3
|
||||
|
||||
|
สำหรับความคิดผมก็วาดกราฟเอาก็จะง่ายเหมือนกันครับ ส่วนการหาdomain gof,fogผมคิดว่าเขียนฟังก์ชันfog,gofแล้ว เขียนเงื่อนไขทั้งหมดที่ได้ เช่น ใต้รูทมากกว่าเท่ากับ0เป็นต้นครับ
__________________
Impossible is nothing |
|
#4
|
||||
|
||||
|
ควรหาจากนิยามดีกว่าครับปลอดภัยที่สุด \( D_{fog} = \{ x \mid x \in D_g \text{ และ } g(x) \in D_f \} \)
ส่วน \( R_{fog} \) ก็ให้หา โดเมนมาก่อนแล้วหาฟังก์ชัน fog เสร็จแล้วค่อยพิจารณา
__________________
PaTa PatA pAtA Pon! |
|
#5
|
||||
|
||||
|
ช่วยแสดงวิธีการหา Range gofโดยละเอียดทีครับ
__________________
Impossible is nothing |
|
#6
|
|||
|
|||
|
จากข้างบน $R_{g\circ f}=\{g(x)\mid x\in[1,2]\}$ และจาก $g(x)=\sqrt{4-x^2}$ จะสามารถหา $R_{g\circ f}$ ได้ทันทีโดยไม่ต้องหา $(g\circ f)(x)$ ออกมาเลยครับ
|
|
#7
|
||||
|
||||
|
ผมลองกลับไปคิดโจทย์ข้อนี้ดู และแสดงวิธีทำออกมา ซึ่งผมได้คำตอบตรงกับที่พี่ warut เฉลย แต่ไม่แน่ใจว่า วิธีการที่ผมทำมานั้นถูกต้องหรือไม่ ดังนั้นผมขอให้พี่ warut กรุณาช่วยตรวจสอบวิธีทำของผมด้วยนะครับว่าถูกต้องหรือไม่
  |
|
#8
|
||||
|
||||
|
.
 |
|
#9
|
||||
|
||||
 |
|
#10
|
||||
|
||||
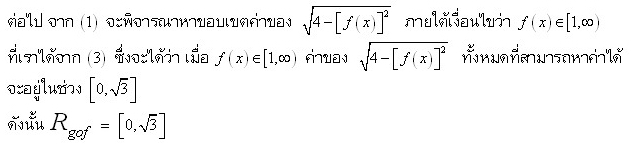 |
|
#11
|
|||
|
|||
|
เท่าที่ดูผมก็ว่าใช้ได้นะครับ ยกเว้นตรงแก้อสมการ $\frac{1}{1-x^2}\le4$ คูณไขว้ไปเลยน่าจะง่ายกว่า เพราะเรารู้ว่าเมื่อ $x\in(-1,1)$ แล้ว $1-x^2>0$
คนอื่นๆมีความเห็นอย่างไรกันบ้างครับ เกี่ยวกับการหา $D_{g\circ f}$ และ $R_{g\circ f}$ ตามแบบของน้อง Eddie  |
|
#12
|
||||
|
||||
|
สำหรับวิธีการหา โดเมน กับ เรนจ์ ของ g o f ปกติแล้ว ผมจะไม่หา g o f ออกมา เพราะเกินความจำเป็น เดี๋ยวว่าง ๆ (ไม่รับปาก 100%) ผมจะตั้งโจทย์ดักทางให้ลองทำนะครับ อาจจะเจอข้อบกพร่องก็ได้
แนวทางของผมในการหา คือ 1. หา $D_f = (-1, 1)$ , $R_f = [1, \infty)$ 2. หา $R_g = [0, 2]$ , $D_g = [-2, 2]$ 3. หาตัวเชื่อม คือ $R_f \cap D_g = [1, 2]$ การหา $D_{g o f}$ ทำได้ 2 ทาง คือ 1. หาโดยนิยาม $D_{g o f} =$ { x | x $ \in D_f \quad \cap f(x) \in D_g$ } 2. หาโดยความเข้าใจ คือ ให้มองว่า $R_f \cap D_g$ เป็น y ของ f คือ $1 \le y \le 2$ หรือ $1 \le \frac{1}{\sqrt{1-x^2}} \le 2$ จากนั้นแก้อสมการออกมา และหากมีที่เกิน $D_f$ ก็ให้นำไปอินเตอร์เซ็กกับ $D_f$ ก็จะ้เป็นคำตอบ สำหรับการหา $R_{g o f}$ หาโดยใช้ความเข้าใจ กล่าวคือ มองว่าตัวเชื่อม $R_f \cap D_g$ เป็น x ของ g คือ $1 \le x \le 2$ จากนั้นก็ให้พยายามจัดรูปให้เหมือนกัน y ของ g คือ $\sqrt{4-x^2}$ และถ้าผลลัพธ์ที่ได้เกิน $R_g$ ก็ให้นำไปอินเตอร์เซ็กกับ $R_g$ ก็จะ้เป็นคำตอบ 
__________________
The Lost Emic <<-- หนังสือเฉลยข้อสอบระดับประถมนานาชาติ EMIC ครั้งที่ 1 - ครั้งที่ 8 ชุดสุดท้าย หลงมา 
16 กุมภาพันธ์ 2006 19:08 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ gon |
|
#13
|
||||
|
||||
|
อีกวิธีหนึ่งที่อยากจะถามคือว่าผมก็คิดได้ครับโดยใช้วิธี ทำจากโดเมนไปหาเรนจ์ได้เสมอหรือป่าวครับ?
__________________
Impossible is nothing |
  |
|
|