ตะลุยโจทย์ Integrate
 

คือ ผมอยากได้โจทย์อินทิเกรตที่ไม่ยาก และง่ายเกินไปอะครับ
เช่นอินทิเกรตตรีโกณ หรือพวก exponential อะครับ
ถ้าผมทำไม่ได้จริงๆ ช่วยสอน step by step ด้วยครับ
ขอบคุณครับ :please:

ผมอ่านแล้วมันไม่ได้ทำเองเลยอะครับ มีโจทย์แล้วก็เฉลยเลย

ยังไงก็ขอโจทย์แบบที่ยังไม่มีเฉลยก่อนด้วยนะครับ

ขอบคุณครับ

$$\int \frac{dx}{1+\sin x} $$

อา ก็แอบจดโจทย์มาก่อน อย่าเพิ่งไปมองเฉลยจิคับ
ถ้าแอบเห็นก่อนก็จดเสดแล้วรอให้ลืมแล้วค่อยกลับมาทำ ตัวอย่างใน บทความมีเยอะ เลย ไม่ต้องหาไกล

เพิ่มเติมให้ต่อจากคุณ warut ครับ

\[ \int \frac{e^x-e^{-x}}{e^x + e^{-x}} dx \]
\[ \int \frac{1}{\sin x} dx \]
\[ \int \sec^3 x \ dx \]


ที่นี่ก็มีตัวอย่างพร้อมแบบฝึกหัดบ้างครับ

ลองทำครับ
$$ \int \frac{e^x-e^{-x}}{e^x+e^{-x}}dx $$
ให้ $ u =e^x+e^{-x} $
$$ \frac{du}{dx}=e^x-e^{-x} $$
$$ \int \frac{du}{u}=\ln|u|+C $$
$$ \int \frac{e^x-e^{-x}}{e^x+e^{-x}} dx=\ln|e^x+e^{-x}|+C $$

:laugh:

$$\begin{array}{rcl} \int \frac{dx}{1+\sin x}&=&\int\frac{1-\sin x}{1-\sin^2x}\ dx\\
&=&\int \frac{1-\sin x}{\cos^2x}\ dx\\
&=&\int \sec^2x\ dx -\int \tan x\sec x \ dx\\
&=&\tan x - \sec x+C \\
\therefore \int\frac{dx}{1+\sin x} &=&\tan x -\sec x +C\end{array}$$

$$\int \frac{dx}{\sin x} = \int \csc x\ dx=\ln|\csc x - \cot x|+c$$

Hint : use integration by part : \( \int u dv = uv - \int v du \)
Let : \( u =\sec x \; \text{and} \; dv=\sec^2 x \ dx\)

ทำไม่ได้อะครับ

Let : \( u =\sec x \; \text{and} \; dv=\sec^2 x \ dx\)
then \( v=\int \sec^2 x \ dx = \tan x \)
ทำการอินทิเกรตทีละส่วน
\[ \begin{array}{rcl} \int \sec^3 x \ dx &= & \sec x \tan x - \int \tan x \ d(\sec x) \\
& = & \sec x \tan x - \int \tan^2 x \sec x \ dx \\
& = & \sec x \tan x - \int (1+ \tan^2 x) \sec x \ dx \\
& = & \sec x \tan x - \int \sec^3 x \ dx + \int \sec x \ dx \\ 2 \int \sec^3 x \ dx & = & \sec x \tan x - ln \mid \sec x +\tan x \mid + C \\
\int \sec^3 x \ dx & = & \frac{1}{2} \sec x \tan x - \frac{1}{2} \ln \mid \sec x +\tan x \mid + C
\end{array} \]

ขอบคุณมากครับ

อยากได้โจทย์ที่เป็นเทคนิคพิเศษ, ใช้บ่อยๆ หรือ ทำแล้วได้ข้อคิดอะครับ

ท่านใดที่มีข้อเสนอแนะหรือเกร็ดความรู้ก็เชิญลงได้เลยครับ

ขอบคุณครับ

แปะไว้ให้ 2 ข้อนะครับ

$$ \int_{0}^{\frac{\pi}{2}} (\sin 2x) \ln (\tan x) dx $$

$$ \int_{0}^{16} \frac{\sqrt[4]{x}}{1+\sqrt{x}} dx $$

ช่วยแปะครับ

$\displaystyle{ \int_{0}^{\frac{\pi}{2}} \frac{\sin^3{x}}{\sin^3{x}+\cos^3{x}}}dx$

ของพี่ nooonuii ไม่มี hint ออกจะโหดไปหน่อยนะครับ ผมเพิ่มให้ละกัน
Hint : first show that \[ \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin^3x +\cos^3 x} dx = \int_0 ^{\frac{\pi}{2}} \frac{\cos^3 x}{\sin^3x +\cos^3 x} dx \]
and use this result to calculate \[ \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin^3x +\cos^3 x} \]

...

Hint เพิ่มเติม $\sin{(\frac{\pi}{2}-x)}=\cos{x}$ :D

เฉลยละกันนะคับ
เราแสดงได้ว่า \[ \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin^3x +\cos^3 x} dx = \int_0 ^{\frac{\pi}{2}} \frac{\cos^3 x}{\sin^3x +\cos^3 x} dx \]
ดังนั้น \[ \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin^3x +\cos^3 x} dx + \int_0 ^{\frac{\pi}{2}} \frac{\cos^3 x}{\sin^3x +\cos^3 x} dx = 2 \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin^3x +\cos^3 x} dx \]
จะได้ว่า \[ \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x + \cos^3 x}{\sin^3x +\cos^3 x} dx = 2 \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin^3x +\cos^3 x} dx \]
ดังนั้น \[ \int_0 ^{\frac{\pi}{2}} \frac{\sin^3 x }{\sin^3x +\cos^3 x} dx = \frac{1}{2} \frac{\pi}{2} = \frac{\pi}{4} \]

สำหรับ Hint ในส่วนของผม

ข้อแรกของผม กับคำถามของคุณ nooonuii ใช้หลักการเดียวกันครับ และเป็น useful trick มากสำหรับอินทิกรัลจำกัดเขตบางประเภท

Trick ที่ว่าคือ

$$ \int_{0}^{a} f(x) dx=\int_{0}^{a} f(a-x) dx $$

ซึ่งพิสูจน์ได้ไม่ยาก โดย ให้ $ u=a-x $

ส่วนข้อที่ 2 แนะนำให้ลองใช้ฟังก์ชันตรีโกณมิติ มาช่วยครับ :cool:

ฟังก์ชันไหนอะครับ มีเยอะแยะไปหมด

ช่วยใบ้ข้อ 2 ของคุณ passer-by: $\sec^2x=1+\tan^2x$
ข้อของคุณ nooonuii หากแสดงได้ว่าสองอินทิกรัลเท่ากัน อาจเขียนได้ว่า $\int\frac{\sin^3x}{\dots}\ dx=\int\ dx-\int\frac{\cos^3x}{\dots}\ dx$ แล้วทำต่อเหมือนคุณ M@gpie ก็ได้ครับ

ไหนๆก็เข้ามาตอบแล้ว ขอแปะโจทย์เพิ่มอีกข้อ หวังว่าคนทำคงไม่บ้าไปซะก่อน :P
$$\int_1^2 \sqrt[4]{2+\sqrt{2x-1}}\,dx$$

ลองทำนะครับ...
ให้ $\sqrt[4]{x} = \tan u $
$$\begin{array}{rcl}\int \frac{\tan u}{1+\tan^2u}\ d(\tan^4u)&=&\int\frac{\tan u}{ \sec^2u} d(\tan^4 u)\\
\because\quad d(\tan^4u)&=& 4\tan^3u\sec^2u \ du\\
ดังนั้น \quad \int \frac{\tan u}{\sec^2u}\ d(\tan^4u)&=&\int 4\tan^4u\ d u\\
\because\quad \int \tan^4u\ du&=&\int (\sec^2u-1)\tan^2u \ du \\
&=&\int\sec^2u\tan^2u\ du-\int\tan^2u \ du \\
&=&\int\tan^2u\ d(\tan u)-\int\sec^2u\ du+\int \ du\\
&=&\frac{\tan^3u}{3}-\tan u +u+C\\
\int 4\tan^4u\ du&=&4(\frac{\tan^3u}{3}-\tan u +u+C)\\
\because \ u&=&\arctan\sqrt[4]{x}\\
\int \frac{ \sqrt[4]{x}}{1+\sqrt x}&=&4\big(\frac{x^{3/4}}{3}-\sqrt[4]{x}+\arctan{\sqrt[4]{x}}\big)\\
\therefore \int_0^{16} \frac{ \sqrt[4]{x}}{1+\sqrt x}&=&4(\frac{8}{3}-2+\arctan 2)\\
&=&4(\frac{2}{3}+\arctan 2 )
\end{array}$$

กว่าจะได้ 1 ข้อ :wacko:
Edit: แก้ขอบเขตครับ

ถูกแล้วล่ะครับ น้อง Mastermander :great: แต่มี comment นิดเดียว ตรงการเขียนขอบเขตของ u กับ x อย่าเอามาปนกัน ก็จะดีนะครับ

งั้นแถมให้อีกข้อนึง

(VTRMC 2005) Compute $ \int_{0}^{1} (e-1)\sqrt{ln(1+ex-x)}+e^{x^{2}} dx $

hint ให้นิดนึงว่า trick ที่ใช้ในข้อนี้ คล้ายๆกับ โจทย์บางข้อ เมื่อปลายปีที่แล้ว

เนื่องจากโจทย์ของคุณ Passer-by ผมทำไม่ได้แน่นอน ผมจึงเอาไปถามในเว็บบอร์ดวิชาการแล้วได้ความมาว่า


ซึ่งทำโดยคุณ GFK
แล้วผมยัง งงๆอยู่ ตรงบรรทัดที่ ---** ทำไมขอบเขตเป็น 1 ถึง e ครับ

1 และ e เป็นค่าของ u เมื่อ x=0 และ 1 ครับ

ก่อนจะเฉลยข้อที่แล้ว แบบไม่ใช้ by parts ขอแปะให้อีกข้อนะครับ คราวนี้ ง่ายกว่าสามข้อแรกของผมหลายเท่าตัว และคงจะเป็นข้อสุดท้ายของผมแล้ว เพราะไม่รู้จะถามอะไรต่อดี :sweat:

Compute $ \int_{0}^{\pi/2} \frac{\sin^{2}(x)}{(1+\cos x)^{2}}\, dx $

ส่วนข้อก่อนหน้านี้ ใช้หลักการเดียวกับ ข้อสอบสมาคม 2548 ข้อ34 คือมองฟังก์ชันเดียวกัน เป็น 2 มุมมอง

จาก $ y= e^{x^{2}}$ ดังนั้น $ x= \sqrt {lny} $

ทำให้ $ \int_{0}^{1} e^{x^{2}} dx + \int_{1}^{e} \sqrt {lny} \, dy= \text{LOWER} +\text{UPPER}= (1)(e)=e $
(LOWER+ UPPER= พื้นที่สี่เหลี่ยมผืนผ้า)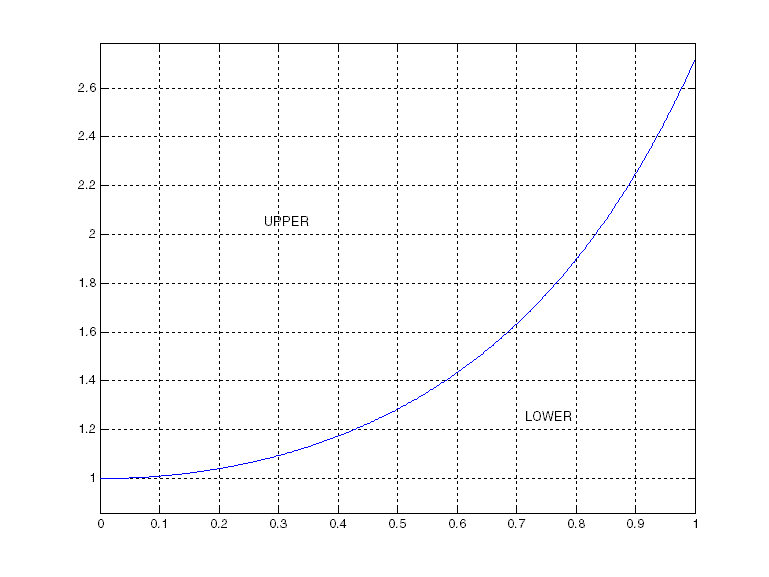

$$\int_0^{\pi/2}\frac{\sin^2x}{(1+\cos x)^2}dx=\int_0^{\pi/2}\frac{4\sin^2\frac{x}{2}\cos^2\frac{x}{2}}{4\cos^4\frac{x}{2}}dx$$

$$\int_0^{\pi/2}\tan^2\frac{x}{2}\ dx = 2\int_0^{\pi/2}\sec^2\frac{x}{2}d(\frac{x}{2})-\int_0^{\pi/2}1\ dx$$

$$=[2\tan \frac{x}{2} - x]|_0^{\frac{\pi}{2}}=2-\frac{\pi}{2}$$

ถูกมั้ยครับ (อุตส่าห์ทำได้)

ถูกแล้วล่ะครับ น้อง Mastermander :great:

แล้วอย่าลืม คำถามของคุณ nongtum ด้วยนะครับ

ส่วนที่ผมบอกว่า ข้อที่แล้ว เป็นข้อสุดท้าย ถือเป็นโมฆะแล้วกันนะครับ เพราะลืมไปว่า ยังเหลือที่อยากถาม อีกข้อนึง (ไม่ถามล่ะเสียดายตายเลย)

Compute $ \int_{0}^{1} \frac{\arcsin x}{x} dx $

ข้อนี้ จะเป็นข้อสุดท้ายของผม จริงๆแล้วล่ะครับ

(Hint : ข้อนี้ ใช้ By parts มาช่วย ประกอบกับ useful trick ที่เคยให้ไป)

P.S. อีก 3 วัน จะกลับมาดูความคืบหน้าข้อนี้นะครับ

$$ \int_0^1 \frac{\arcsin x}{x}dx $$
Let $ x=\sin u$
$$\begin{array}{rcl}\int \frac{\arcsin x}{x}dx&=&\int \frac{u}{\sin u}d(\sin u)\\
&=&\int u (\cot u) du\\
&=&\text{what next}\end{array}$$

คือผมไปถามรุ่นพี่เอาแล้วได้ความมาว่า $\int \frac{\arcsin{x}}{x}dx=x $ ใช่หรือเปล่าครับ

ยังไม่ได้ทดนะครับ แต่ลองอินทิเกรตแยกส่วนด้านบนดูนะครับ อ่าจต้องหา $\int\cot x\ dx$ มาเก็บไว้ก่อนด้วย

ผมว่าคงไม่ใช่แน่ๆครับ ในความเห็นของผม น่าจะไม่มี explicit formula สำหรับ integrand ตัวนี้

ตอนนี้ ก็ครบ 3 วันแล้ว งั้นผมเฉลยแบบละเอียดๆ เลยนะ


ส่วนที่ 1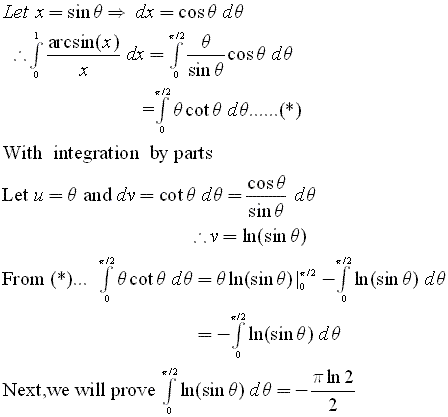


ส่วนที่ 2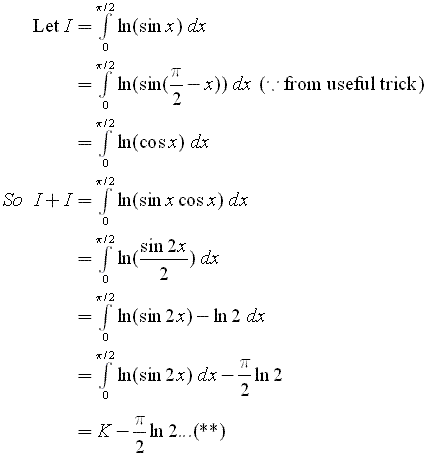


ส่วนที่ 3

ตัวปัญหาของผมคือ

$$ \int \ln(\sin x )\ dx=? $$

ตอนนี้ คำอธิบาย 3 ส่วนด้านบน สมบูรณ์ เรียบร้อยแล้วครับ

็สงสัยว่า...

$$ \int_{\pi/2}^{\pi}\cos(\pi/2- u)\ du=\int_0^{\pi/2}\cos y \ dy $$

ทำไมขอบเขตเปลี่ยนไป

ผมสงสัยนิดนึงว่า ตอนเราเปลี่ยนตัวแปร มันจะมีปัญหาที่ \( \theta = \frac{\pi}{2} \; \) รึเปล่าครับ
เพราะว่า มันจะทำให้ ฟังก์ชัน \( \ln( \sin ( \frac{\pi}{2}- \theta )) \) หาค่าไม่ได้

จริงๆแล้วมันมีปัญหาตั้งแต่ก่อนเปลี่ยนตัวแปรแล้วครับ ซึ่งก็คือที่ $\theta=0$ ทั้งนี้เพราะโจทย์ข้อนี้มันเป็น improper integral น่ะครับ ไม่รู้ตอบตรงประเด็นรึเปล่า :rolleyes:

ว่าแล้วก็แถมโจทย์ให้อีกข้อครับ $$\int x^n\ln x \,dx$$ โดยที่ $n$ เป็นจำนวนจริงบวก

ที่ขอบเขตเป็นอย่างนั้นเพราะว่า cosq=cos(-q) และเราให้ y=u-(p/2) เหมือนที่ผมเขียนแนบไว้ข้างๆบรรทัดในวิธีทำ น่ะครับ
เมื่อ u=p/2 ก็จะได้ y=0 และเมื่อ u= p ก็จะได้ y= p/2

P.S. สรุปว่า เรากำลัง จะสร้างกระทู้ integrate มาราธอน กันใช่มั้ยครับ :laugh:

โจทย์ยากๆทั้งนั้นเลย

what is improper integral ??

มาราธอนเลยก็ดีครับ

What is improper integral ?? ---> read this

คุณ warut ไม่มาเฉลยสักหน่อยหรอครับ

อยากได้โจทย์ by part ครับ

เพิ่งเห็นสูตรของ $ \int \ln x \ dx $
ขอลองทำของคุณ warut ดูนะครับ
Let u = ln x , dv = xⁿ dx
$$\begin{array}{rcl} \int x^n\ln x\ dx&=&\frac{x^{n+1}\ln x}{n+1}-\frac{1}{n+1}\int x^{n+1}d \ln x \\
&=&\displaystyle{\frac{x^{n+1}\ln x}{n+1} -\frac{\int x^n\,dx}{n+1}} \\
\int x^n\ln x\ dx&=&\displaystyle{ \frac{x^{n+1}\ln x}{n+1}-\frac{x^{n+1}}{(n+1)^2}+c }\end{array}$$

Edit : เปลี่ยน u ,v

ถูกครับ แต่คำตอบยังสามารถ simplify ได้อีกหน่อยเป็น $$ \frac{x^{n+1}\ln x}{n+1}- \frac{x^{n+1}}{(n+1)^2} $$ และวิธีที่ใช้ก็ยังไม่ใช่วิธีที่ตรงไปตรงมาที่สุด ทำแบบ ความเห็นเพิ่มเติมที่ 107 ในกระทู้ที่ วิชาการ.คอม จะดีกว่าครับ

สำหรับสูตรของ $\int\ln x\,dx$ หาได้โดยใช้ integration by parts (ต้องมี s เสมอนะครับ) ดังนี้ $$\int\ln x\,dx= x\ln x-\int x\,d(\ln x)= x\ln x-\int1\,dx= x\ln x-x+C $$