สำหรับคนชอบตรีโกณครับ
 

จงหาค่าของ
cos p/5 * cos 2p/5 * cos 3p/5 * cos 4p/5

รอมานานครับสำหรับกระทู้แบบนี้ หาคนตั้งมิได้เลย เอามาฝากด้วยอีกคนครับ. เอกลักษณ์ที่เก็บดองเอาไว้ เรียกน้ำย่อยกันด้วย ดูว่ามีใครชอบตรีโกณกันจริงบ้าง

1) จงพิสูจน์ว่า cos³(2p/13) + cos³(4p/13) + cos³(6p/13) + cos³(8p/13) + cos³(10p/13) + cos³(12p/13) = -1/2

จากนั้นก็ตามด้วยอาหารเบา ๆก่อน
2) จงพิสูจน์ว่า sec(2p/13) + sec(4p/13) + sec(6p/13) + sec(8p/13) + sec(10p/13) + sec(12p/13) = 6


3) จงพิสูจน์ว่า sec³(2p/13) + sec³(4p/13) + sec³(6p/13) + sec³(8p/13) + sec³(10p/13) + sec³(12p/13) = 552

ถ้าชุดแรกยังไม่อิ่ม ก็ต่ออีกจาน
4) จงพิสูจน์ว่า sec³(2p/17) + sec³(4p/17) + sec³(6p/17) + sec³(8p/17) + sec³(10p/17) + sec³(12p/17) + sec³(14p/17) + sec³(16p/17) = 1232

ถ้ายังไม่หนักท้อง ก็ต่อด้วยนี่เลย
5) จงพิสูจน์ว่า
sec(p/27) + sec(5p/27) + sec(7p/27) + sec(11p/27) + sec(13p/27) + sec(17p/27) + sec(19p/27) + sec(23p/27) + sec25(p/27) = 18
(Hint : ละมั้ง cos(p/27) + cos(5p/27) + cos(7p/27) + cos(11p/27) + cos(13p/27) + cos(17p/27) + cos(19p/27) + cos(23p/27) + cos25(p/27) = 0)

6) จงพิสูจน์ว่า sec³(p/27) + sec³(5p/27) + sec³(7p/27) + sec³(11p/27) + sec³(13p/27) + sec³(17p/27) + sec³(19p/27) + sec³(23p/27) + sec³(25p/27) = 5112

หมายเหตุ . ปัญหาเหล่านี้ล้วนแล้วแต่ ผ่านการทำมาด้วยมือแล้วทั้งสิ้น ดังนั้นจึงมั่นใจได้ว่าทำได้แน่ ๆ เดี๋ยวว่าจะเอาเอกลักษณ์แบบ p/44 หรือ p/108 มาใส่

เอาแบบ p/102 ล่ะกัน แค่พิมพ์ก็เหนื่อยแล้ว แต่ก็อยากให้เห็นและลองทำกันดูนะครับ.

จงพิสูจน์ว่า
sec(p/102) + sec(11p/102) + sec(13p/102) + sec(23p/102) + sec(25p/102) + sec(35p/102) + sec(37p/102) + sec(47p/102) + sec(49p/102) + sec(59p/102) + sec(61p/102) + sec(71p/102) + sec(73p/102) + sec(83p/102) + sec(85p/102) + sec(95p/102) + sec(97p/102) = 34/ึ3

ท่าจะหาคนชอบตรีโกณไม่ได้เลย ไม่เป็นไรลงให้ดูเล่น ๆ อีกหนึ่งชุด
sec(p/740) + sec(39p/740) + sec(41p/740) + sec(79p/740) + sec(81p/740) + sec(119p/740) + sec(121p/740) + sec(159p/740) + sec(161p/740) + sec(199p/740) + sec(201p/740) + sec(239p/740) + sec(241p/740) + sec(279p/740) + sec(281p/740) + sec(319p/740) + sec(321p/740) + sec(359p/740) + sec(361p/740) + sec(399p/740) + sec(401p/740) + sec(439p/740) + sec(441p/740) + sec(479p/740) + sec(481p/740) + sec(519p/740) + sec(521p/740) + sec(559p/740) + sec(561p/740) + sec(599p/740) + sec(601p/740) + sec(639p/740) + sec(641p/740) + sec(679p/740) + sec(681p/740) + sec(719p/740) + sec(721p/740) = 148 / [ (3 + ึ5)^1/2 + (5 - ึ5)^1/2 ]

:eek: ยาวเกินไปครับกว่าจะได้คำตอบมาตาลายไปหมดแน่ๆเลย ลองเข้าไปอ่านวิธีคิดในบทความแล้วครับ เยี่ยมมากๆเลย

ตอนนี้พี่กำลังพัฒนาทฤษฎีบททางตรีโกณมิติหลาย ๆ อย่างขึ้นมาครับ. ที่เขียน ๆ ไว้ในบทความนั่นของเก่านานแล้ว คงใช้แก้ข้อล่าง ๆ ลงมาไม่ได้ ส่วนของใหม่กำลังลุยไปเรื่อย ๆ ว่าจะเลิกคิดแล้วนะหยุดไม่ได้สักที ก็ของมันชอบ ถ้าสำเร็จอาจจะได้เอกลักษณ์ของรากที่ 5 หลุดออกมา(หวังว่ามันคงจะหลุดออกมาสักหนึ่ง)

ยากจัง ตาลาย

บทความของท่าน กรเยี่ยมมากๆครับ ยกนิ้วให้เลยครับ ขอรบกวน ท่านกร ที่เคารพอีกนิดหนึ่งนะครับ ไม่ทราบว่าอยากจะได้เอกสาร ต่างๆที่นักเรียน อบรมค่ายวิชาการโอลิมปิกต้องไปหาที่ไหนครับ หรือ ต้องไปโหลดมาจากเว็ปไหนครับ แล้วข้อสอบทุน คิง กับทุน กพ ด้วยครับ อยากให้เอามาลงเร็วๆครับ วิญญานแห่งคณิตศาสตร์ จะคุ้มครอง ท่าน กร ตลอดไปครับ ขอให้แข็งแรง มีเงินใช้เยอะๆนะครับ...อิอิอิ

ขออภัยด้วยครับ ที่คำถามผมคุมเครือ ผมหมายถึง เนื้อหาหลักสูตร ทั้งหมดที่ นักเรียนค่ายคณิตโอลิมปิกเขาเรียนกัน ผมสามารถหามาอ่านได้จากที่ไหนครับ ขอคุณล่วงหน้าครับ

สสวท. ทำเป็นเล่มเล็กๆออกขายอยู่ครับ รู้สึกว่าจะมี 6-7 เรื่องนะครับ ไม่แน่ใจว่ายังมีอยู่หรือเปล่า เนื้อหาอาจจะยังไม่สะใจโจ๋ซักเท่าไหร่ แต่ช่วยปูพื้นฐานให้เราดีพอสมควรครับ เนื้อหาก็ครอบคลุมค่ายของสสวท.รอบ 25 คนสุดท้ายครับ แต่รอบลึกๆกว่านั้นต้องหาจากคนที่เคยเข้ารอบน่ะครับ เพราะจะมีเนื้อหาเพิ่มเติมอีก

ขอบคุณมากครับ คุณ nooonuii แล้วเนื้อหาทั้งหมดสามารถหาได้จากเว็บไซด์ไหน ได้บ้างครับ คืออยากเรียนอะครับ แต่สอบไม่ถึงรอบลึกๆ จะทำไงดีครับ

อย่างที่ noonuiii ว่าไว้ครับ. สสวท. ทำออกมาแล้วหลายเล่ม ที่นับ ๆดูจากสมองก็มี
- ทฤษฎีจำนวน
- อสมการ
- คอมบินาทอริค
- สมการเชิงฟังก์ชัน
- สมการ เอ๊ะหรือ พีชคณิต หรือ อะไรสักอย่างแนวนี้
- เรขาคณิต

อืม. หมดหรือยังนึกก่อนครับ. นึกออกจะมาเติมอีก ส่วนหลักสูตรเนื้อหาหลัก ๆ ก็ตามที่เขียนข้างบน โดยแต่ละเรื่องก็มีขอบข่ายลงไปว่าลึกในระดับไหน ส่วนเนื้อหาทั้งหมดที่ สสวท. ใช้ติวนั้น ถ้าความจำผมยังดีอยู่ จะมีบอกในที่เว็บ สสวท. ครับ ประมาณเป็น Course Outline หัวข้อต่าง ๆ เป็นเกินร้อยกว่าหัวข้อ ส่วนจะสอนได้ทันแค่ไหนก็ว่าอีกที ลองไปควานหาในเว็บ สสวท.นะครับ.

สำหรับถ้าต้องการ Download เนื้อมาอ่าน. โอ้. อันนี้มีเพียบครับ. ในเครื่องคอมผมก็มีจนไม่รู้จะอ่านตรงไหนก่อนดี ข้อสอบทั่วโลกมหาศาล เนื้อหาแบบเป็น Journal ก็มี แบบเป็น E- book เป็นเล่ม ๆ ก็เยอะ เวลา Search ก็แนะว่า ให้พิมพ์คำว่า pdf หรือ ps (ใช้ gsview เปิด) นำหน้าด้วย ต่อไปนี้เป็นตัวอย่าง E-Book ที่เป็นเล่ม ๆ แนะนำว่าให้ Download ลงมาที่เครื่องก่อนนะครับ.ใช้โปรแกรมประเภท Flashget

โดย Kiran Kedlaya

note on Euclidean Geometry : http://www.unl.edu/amc/a-activities/...neqs-080299.ps

Lecture on อสมการ "A is less than B" : http://www.unl.edu/amc/a-activities/...neqs-080299.ps
เล่มนี้สุดยอดเช่นกัน

อีก 2 เล่มเป็น E - Book : style probleming solving มีปัญหาในแต่ละเล่มทั่วโลกพร้อมเฉลย มหาศาล
Mathematical Olympiads 1995-1996: Olympiad
Problems from Around the World : http://www.unl.edu/amc/a-activities/...6-97-01feb.pdf (อันนี้เป็น files.ps ก็มี)

Mathematical Olympiads 1996-1997: Olympiad
Problems from Around the World : http://www.unl.edu/amc/a-activities/...7-98-01feb.pdf อันนี้เป็น files.ps ก็มี)


ถ้าจำไม่ผิด 2 เล่มหลังเป็นของ Paul Zeitz นัก Solve ปัญหาแนวโอลิมปิก ที่ทำออกมาทุกปี ตีพิมพ์โดย MAA ไม่รู้ใครทำเป็น pdf กับ ps ออกมา หรือ เป็นความจงใจแจกแจง ที่แน่ ๆ รู้กันไปทั่วโลกแล้วครับ. ดูรูปเขาได้ที่ http://mathcircle.berkeley.edu/

ก็คงพอหอมปากหอม. ลองอ่านเท่าที่มีอยู่ให้จบก่อน ถ้าอ่านแล้วไม่เข้าใจ อาจจะลองหาเล่มอื่นในเน็ต มีเต็มครับ. ใช้ให้เป็นเท่านั้นเอง

พี่ gon คับ คือ file .ps มันต้องใช้อะไรเปิดหรอคับ คอมที่บ้านผมมันเปิดไม่ได้คับ

สมัยผมเรียน เนื้อหาที่ใช้อบรมมีดังนี้ครับ

• Logic and Proofs
• Plane Geometry
• Inequalities
• Combinatorics
• Number Theory
• Algebra

เอกสารประกอบ การเตรียมตัวสอบโอลิมปิก ของต่างประเทศก็มีครับ เช่นที่
Contest Resources รวบรวมไว้เยอะพอสมควร แต่ตอนนี้ผมเข้าเว็บนี้ไม่ได้แล้ว คงเหลือแต่ซากของมันใน Google แต่คิดว่าลิงก์ไปยังเอกสารอื่นๆ ยังคงอยู่ครบ

สำหรับไฟล์ ps หากเรามี Acrobat เวอร์ชันเต็ม เมื่อเรียกใช้งานไฟล์ ps โปรแกรม Acrobat Distiller จะแปลงจาก ps เป็น pdf ให้อัตโนมัติครับ แต่ส่วนใหญ่จะได้ผลลัพธ์ที่ไม่น่าประทับใจ (เมื่อ Acrobat Distiller หาฟอนต์ที่ตรงกับใน ps ไม่ได้ จะใช้ฟอนต์อื่นแทน)

ดังนั้น โดยทั่วไปจะใช้โปรแกรม GSview เปิดอ่าน (GSview เปิดไฟล์ pdf ได้ด้วย) ก่อนจะใช้งาน GSview จะต้องติดตั้งโปรแกรม Ghostscript ก่อนครับ (GSview เป็น GI ของ Ghostscript)

• Ghostscript 8.14
• GSview 4.6

นอกจาก ฟอร์แมท ps และ pdf แล้ว อีกฟอร์แมทหนึ่งที่พบได้บ่อยคือ dvi ครับ อันนี้เป็นผลิตผลของ LaTeX ครับ (ไม่ใช่กาว LaTeX นะครับ :) แต่เป็นโปรแกรมเรียงพิมพ์แบบหนึ่ง) ต้องใช้โปรแกรมพวก dvi viewer เปิด ผมก็ไม่ทราบว่ามีโปรแกรมเปิดดูแบบอิสระหรือไม่ แต่หากใครติดตั้งโปรแกรมสำหรับเขียน LaTeX เช่น MiKTeX จะมีโปรแกรม Yap ใช้เปิดอ่านได้ครับ และมี dvips ใช้แปลงจาก dvi เป็น ps ได้อีกด้วย

ต้องกราบเท้าขอบพระคุณ ท่าน กร และท่าน ท็อป งามๆเลยครับ ขอบพระคุณมากๆครับ ที่แนะนำหนังสือดีๆให้ผมอ่านครับ ทีเว็บไหนดีๆแนะนำผมอีกนะครับ ท่าน พี่ และเพื่อนๆ ทั้งหลาย ขอบคุณครับ!!!

เพิ่งคิดได้สด ๆ ร้อน ๆ เลยครับ. อยากให้ดูกัน :rolleyes:

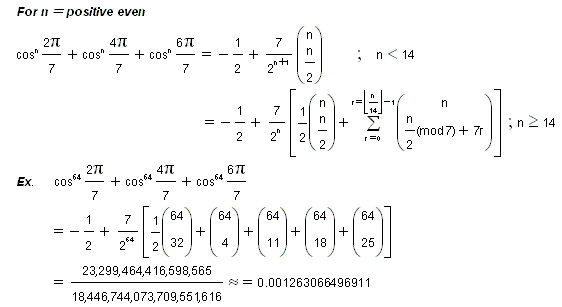พอจะบอกข้อมูลเกี่ยวกับ
การแก้อสมการตรีโกณได้หรืไม่
ว่าหาจากเล่มไหนได้บ้าง
เพราะจากเนื้อหาจะไม่มี
แต่ test ของปีเก่าๆจะมี
ช่วยสร้างเนื้อเรื่องตรงนี้ขึ้นมาด้วยก็จะ
ทำให้เข้าใจได้มากขึ้น

mathematic man register :cool:

พอจะมี ท.บ. เกี่ยวกับอสมการตรีโกณ
ด้วยหรือไม่ เพราะเท่าที่ค้นดู จะไม่มี
ถ้าเป็นไปได้ช่วย ลงมาให้ด้วยได้ก็จะดี
เพราะขนาดเรื่อง ตรีโกณมี ท.บ. เป็นร้อย
แต่พอมา link กับ อสมการ เป็น
อสมการตรีโกณก็ไม่เห็นมีข้อมูล
โผล่ออกมาให้อ่านบ้าง โดยสรุปอยากจะให้
ลงเกี่ยวกับเนื้อหาตรงนี้ด้วย และทำเป็น
ท.บ.ไปเลยก็จะช่วยได้มาก และอยากจะให้ช่วย
ใช้ Ex and solution ไปด้วยในแต่ละ ท.บ.
ก็จะทำให้ได้รับความเข้าใจได้อย่างรวดเร็ว
และคิดว่าเนื้อหาส่วนนี้ก็มีความสำคัญไม่แพ้เรื่อง
สมการตรีโกณเช่นเดียวกันเพราะอะไรงั้นหรือ
มันยากกว่านั่นเองไม่เชื่อลองเทียบระหว่างการแก้สมการ
และการแก้อสมการดูใน ม4 เล่ม1 ขนาดยัง
ไม่มีตรีโกณเข้าไปเกี่ยวก็ยังทำแทบไม่ทันกับเวลา


mathematic man register :cool: :cool: :cool:

เอ่อ. อสมการตรีโกณที่น้องว่ามา หมายถึง ใช้กับข้อสอบระดับไหนหรือครับ. Ent', สมาคม ฯ , โอลิมปิก หรือ สูงกว่านั้น จากที่อ่านมาเข้าใจว่าคงหมายถึง ระดับสอบ Ent' เท่านั้นหรือเปล่า :rolleyes:

ถ้าจะให้พูดถึงหลักการแก้อสมการ โดยทั่ว ๆ ไป ก็เหมือนกับการแก้อสมการในเรื่องจำนวนจริง ถ้าเข้าใจตรงนั้นกระจ่างจริง ตรีโกณมิติก็ทำแบบเดียวกัน เพียงแต่ในเรื่องตรีโกณมิติอาจจะมี ลูกเล่นเพิ่มเติมเล็กน้อย เช่น การแทน cos q ด้วย x และ sin q ด้วย y เพื่อให้ดูง่ายขึ้น เท่านั้น

ลองดูปัญหาพื้นฐานก่อน เช่น
ถ้า cos q ณ 1/2 แล้ว จงหาค่าของ q เมื่อ

ก. 0 ฃ q ฃ 2p ปัญหาแบบนี้ สำหรับน้องถือว่าหมูหรือไม่ ? ถ้าหมูลองขยับเปลี่ยนโดเมนเป็น
ข. -p ฃ q ฃ p กระดูกขึ้นหรือไม่เวลาตอบ และ ถ้าตอบรูปทั่วไปเลย คือ ตอบเป็นหรือไม่

ลองขยับข้ามไป 2 ขั้น คือ เป็น [ sin q - (1/2) ] / (cos²q - cos q) ณ 0 อย่างนี้ถือว่าหมูหรือไม่ ถ้าแค่ระดับสอบ Ent' การ solve ปัญหานี้ได้ด้วยความเข้าใจ น่าจะเพียงพอในการแก้ปัญหาอสมการตรีโกณทุกอย่างแล้ว

จะให้ดีน้องต้องยกตัวอย่างปัญหาที่น้องคิดว่า กระดูก สำหรับน้องให้ดูครับ. พี่จะได้เข้าใจก่อนว่าระดับความรู้ของน้องอยู่ตรงไหน เดี๋ยวคุยกันไม่ถูก อ้อ. ช่วงนี้พี่ยังไม่ว่างทำอย่างที่น้องต้องการครับ. รออีกไม่นาน (ล่ะมั้ง)เดี๋ยวหนังสือที่พี่เขียนอยู่ ก็จะเสร็จแล้ว (ว่าแบบนี้มาหลายปีแล้ว :D )

วันนี้ได้มาเปิดดูตามคำถามที่ถามไว้
ก็เลยเอาโจทย์มาให้ช่วยอธิบาย
เกี่ยวกับอสมการ

1/sin(m) +1/sin^2 (m) +1/sin^3(m) < 1

คืออยากจะให้ช่วยอธิบายรายละเอียดให้ด้วย
และวิธีการ solution ที่ใช้เวลาน้อย
และรวดเร็ว และมีเทคนิคอะไรบ้าง

mathematic man register :cool:

ไม่รู้ว่าทำไมในเนื้อหาจะไม่มีเรื่องนี้
แต่พอไปสอบก็จะพบ
ตามสนามสอบต่างๆ
พอจะแนะนำweb side ที่มีเรื่องนี้ได้บ้างหรือไม่

คือไม่เข้าใจวิธีการแก้อสมการตรีโกณ
โดยปกติถ้าเป็นเรื่องตรีโกณก็รู้เรื่องทั้งหมด
รวมถึงการแก้สมการด้วย
แต่พอเป็นอสมการก็ไม่เห็นจะมี
เนื้อหาเกี่ยวกับส่วนนี้โดยตรงทำให้ไม่สามารถไปศึกษา
ข้อมูลมาใช้ได้
เรื่องโจทย์มีให้เห็นมากมายหลายหลาก
ก็ลองไปถามอาจารย์ดูบ้าง ทีนี้พอไม่อยู่ในเนื้อหาที่
อาจารย์สอน ท่านก็เลยตอบแบบไม่ค่อย clear
ผมจึงคิดว่า ถ้าในข้อสอบต่างๆออกมาได้
ก็น่าจะมีเนื้อหาส่วนนี้ support อยู่ด้วย
เพื่อรองรับกันยังไง แต่ทีนี้พอเอาเข้าจริง
กลับไม่มี ก็หวังท่านพี่นี่แหละเป็น key man
ที่ช่วยแนะนำแทน อาจารย์ที่สอนอยู่ที :cool: :cool: :cool:

mathtermatic man register

อยากรู้เรื่อง สมการกำลังมากกว่าหรือเท่ากับห้าครับ

แล้วก็อยากได้เว็บดีๆอ่านง่ายๆ และเนื้อหาครอบคุมเกี่ยวกับเรื่องของ Abel และ Galois Theory นะคร๊าบ

ในระหว่างที่ยังไม่มีผู้เชี่ยวชาญทางตรีโกณมาตอบ ผมขอตอบให้แทนไปก่อนนะครับ :)

กรณีที่ 1: sin(m) > 0
จะเห็นว่า 1/sin(m) ณ 1 ดังนั้นในกรณีนี้อสมการโจทย์จึงไม่เป็นจริงเสมอ

กรณีที่ 2: sin(m) < 0
จะเห็นว่า 1/sin(m) ฃ -1 ดังนั้นในกรณีนี้อสมการโจทย์จึงเป็นจริงเสมอเพราะ
ถ้า x ฃ -1 แล้ว x³ + x² + x - 1 = x²(x + 1) + x - 1 < 0 เสมอ

สรุปว่าคำตอบคือค่า m ทุกค่าที่ทำให้ sin(m) < 0 (คงหาเองได้นะครับ) :D

:cool:
วันนี้ผมเข้ามาดูคำถาม
ผมพอเข้าใจบ้างแล้วล่ะ
คิดว่าคงพอช่วยได้
วันนี้เลยอยากจะถามเกี่ยวกับโจทย์
อีกบ้างเล็กน้อย
ดังนี้ คือ
:cool:
I . [sin(m)+sin(2m)+sin(3m)]/tan(m) =< 1............A
II . [sin(m)+sin(2m)+sin(3m)]/tan(m) >=1.............B

จงหา (A-B)

ก็เหมือนเคยคืออยากจะถามเทคนิค
concept และวีธีการจากพวกท่านพี่
อีกเช่นเคย ว่าสองข้อนี้ หลักและ
ข้อแตกต่างอย่างไรบ้าง และมีวิธีการ
ร่นเวลาลงได้อย่างไรบ้าง เพื่อช่วย
ประหยัดเวลา

mathematic man register :cool: :cool: :cool:

ข้อนี้คงต้องรอให้คนอื่นมาตอบแล้วล่ะ ผมทำบ่ได้เพราะอ่านโจทย์ไม่เข้าใจอะครับ :confused:

:cool:
คือว่าต้องขออภัยท่านพี่
ที่ไม่ได้ให้รายละเอียด
เลยทำให้เข้าใจคลาดเคลื่อน
คือว่าให้ set A เป็นสมาชิกของ ...........I
และให้ set B เป้นสมาาชิกของ.............II
คือแก้อสมการออกมาให้ได้ในแต่ละข้อ
แล้วต่อไปก็คิดเหมือน เรื่องสมาชิก set
:cool:


mathematic man register :cool: :cool: :cool:

หลักการแก้อสมการ โดยทั่วไป คือ ซ้ายมือแยกตัวประกอบ ขวามือเป็น 0 พจน์ที่แยกตัวประกอบมีกำลังแต่ละวงเล็บเป็น 1, ส.ป.ส ของแต่ละตัวแปรเป็นบวก

หลักการแก้ข้อนี้ :
1. By Sense เรื่องสมมาตรที่ตัวเศษ จะต้องจับเอา sin q + sin 3q กันก่อน แล้วดึงตัวร่วม จากนั้นแปลง tan q กลับสู่สามัญคือ sin q / cos q แล้วแปลงร่าง sin 2q คูณ ๆ ตัด ๆ จึ๊ก พร้อมกับย้าย 1 ไปจะได้ 4cos³q + 2cos² - 1 ฃ 0

2. simplify ปัญหาให้ง่ายขึ้นโดยให้ x = cos q อสมการจึงเป็น 4x³ + 2x² - 1 ฃ 0 จากนั้นมุ่งที่จะแยกตัวประกอบของพจน์ทางซ้ายมือ By sense อีกเช่นกัน นำ 2 คูณตลอดจะได้ 8x³ + 4x² - 2 ฃ 0 ตอนนี้คิดว่าเป็นสมการก็พอก่อน
จากนั้นสมมติให้ y = 2x ก็จะได้ว่า y³ + y² - 2 = 0 สมการนี้ obvious ว่า y = 1 เมื่อนำไป y = 1 ไปหารสังเคราะห์ก็จะได้ (y - 1)[ (y + 1)² + 1 ] ฃ 0 นั่นคือ 2x - 1 ฃ 0 --> cos q ฃ 1/2

ที่เหลือคิดต่อเอาเองนะครับ. ถือว่าจบโดยหลักการแล้ว

:cool: สำหรับผมแล้ว
พอได้
4k^3+2k^2-1 >=0.........1
โดยที่ k=cos(m)

แล้วแทนค่า k=1 พบว่า ..........1 เป็นจริง
แทนค่า k=0 พบว่า...........1 ไม่เป็นความจริง
แทนค่า k=1/2พบว่า...........1 เป็นจริง
ดังนั้นผมสรุปว่า
cos(m) ก็จะอยู่ในช่วง [ 0 ถึง 60]จาก..........1
และ
4k^3+2K^2-1=<0............2
ก็จะสรุปว่าอยู่ในช่วง (60 ถึง 180]จาก..........2

พอผมรู้อย่างนี้แล้วแต่ผมไม่พอใจกับคำตอบแค่นี้
ผมอยากถามว่ามีวิธีแก้ อสมการกำลังสาม
แบบตรงเลยได้มั้ย เพราะผมต้องการ final solution
ที่หาจากสมการ ผมลองแทนค่าดูพบว่ามันแก้ไม่ได้
เพราะจากความรู้เรื่อง ตัวประกอบ มันก็ยังไม่พอ

จึงอยากถามท่านพี่ว่าเราจะแก้จากอสมการโดยตรงไปเลยได้อย่างไร
คือพอจะแยกออกมาเป็นตัวประกอบก่อนได้หรือไม่
เพราะผมใช้ความรู้จากห้องเรียนมันก็ยังหาไม่ได้
คือผมอยากลองแก้แบบตัวประกอบ(cos )(cos )(cos )
3 วงเล็บคูณกันธรรมดาจะได้หรือไม่ :cool:


mathematic man register :cool: :cool: :cool:

:cool:
point ของผมคือว่า
จากการแก้ของท่านพี่
ถ้าไม่คูณ 2 และ ไม่กำหนด ค่า y= 2x
จะสามารถ solution โดยตรงไปเลย
ได้หรือไม่ คือถ้าเราแยกให้เป็น ค่า cos มาคูณกัน
สามวงเล็บตามที่ได้อ้างมาไว้
แต่ต้องขอชมว่า technic by sense ของท่านพี่
มันทำให้ผมเชื่อว่า นี่คือตัวจริง
ขนาดผมยังมองไม่เห็นเลย

mathematic man register :cool: :cool: :cool:

อืม วิธีพี่ gon นี่เหนือชั้นจิงๆ สมเป็นยุทธ์ยอด ตรีโกณ คำนับ 1 ครั้ง
สามารถ solve ตรงๆก็ได้ครับ ไม่ยาก
ปัญหาคือเราต้องแยกตัวประกอบของ
4x&sup3;+2x&sup2;-1 = 0
เราหารตลอด ด้วย 4 จะได้
x&sup3; + x&sup2;/2 - 1/4 = 0
โดยทฤษฎีบทตัวประกอบ
พบว่า มีคำตอบที่เป็นจำนวนจริงคือ x= -1/2
ก็จะได้สมการเป็น
(x+1/2)(x&sup2; +x+1/2)< 0
จะได้ x < -1/2 ได้ผลลัพธ์เหมือนกัน

การแก้อสมการตรีโกณนั้น หลักการเหมือนกับการแก้อสมการทั่วไปเลยครับ แต่ว่ายากตรงที่การตอบซึ่งขึ้นอยู่กับ การกำหนดช่วงของเอกภพสัมพัทธ์ หนังสือม.ปลายไม่ค่อยพูดถึงเรื่องนี้เท่าไร มีแต่ก็ไม่ละเอียดครับส่วนใหญ่จะเป็นตัวอย่างง่ายๆ ลองหาตามหนังสือ text เกี่ยวกับ trigon ดูน่าจะมี

มันแยกได้แค่ 2 วงเล็บเท่านั้นครับ ก็ที่แยกให้ดูแล้วนั่นล่ะครับ. คือ (2cos q - 1)(4cos²q + 4cosq + 2)
ในวงเล็บหลังถ้าจะแยกต่อเป็น 2 วงเล็บ ก็จะต้องใช้จำนวนจินตภาพมาเกี่ยวข้องแล้ว ซึ่งก็ไม่จำเป็นต้องแยกต่อเพราะ ไม่มีการเปรียบเทียบการมากกว่าน้อยกว่าระหว่างจำนวนเชิงซ้อน a + bi เมื่อ b น 0

ส่วนวิธีการที่ให้ y = 2x ที่จริงไม่ใช่เทคนิคอะไรใหม่ครับ. เป็นสิ่งปกติที่ทำกันในทฤษฎีสมการ (Theory of Equation) คือ ถ้าไม่จำเป็นจริง ๆ พี่ก็ไม่จะใช้ ท.บ. คำตอบตรรกยะ เท่าใด เพราะถ้าต้องยุ่งกับเศษส่วนคงไม่สนุกครับ.

Theory of Equation มีเนื้อหาเกี่ยวกับอะไรบ้างหรอคับ พี่กรแนะนำหน่อย ชื่อหนังสือ+คนแต่ง+สถานที่หา

:cool:
หวัดดีครับ หายไปนาน
วันนี้กลับมาดูก็พบกับคำตอบหลากหลาย
ดีมากจริงๆ ที่ได้ discuss กับคน
ที่เก่งทำให้ ผมเข้าใจมากขึ้น
ในตอนนี้ ผมพัฒนาไปถึงขั้น
ไม่ต้องพึ่งพาอาจารย์
ก็สามารถเข้าใจได้

วันนี้ก็มีคำถามอีกเหมือนกัน
แต่ไม่ต้องคำนวณ
คือว่า อยากให้เดาว่า
โจทย์นี้ผมเอามาจากไหน?
และคิดว่ามันยากระดับกี่ดาว :cool:

maththematic man register :cool: :cool: :cool:

โจทย์ข้อนี้เอามาจากไหน แน่นอนว่าพี่ไม่รู้ครับ. เพราะไม่เคยรู้สึกว่าเห็นมาก่อน

ยากระดับกี่ดาว ? อันนี้ต้องแล้วแต่คนครับ. คงฟันธงไม่ได้ แต่ถ้าจะให้พี่จำแนกโดยใช้ความรู้สึกส่วนตัว ก็ยากกว่า Ent' ประมาณ สมาคม ข้อเติมคำตอบ หรือ จะเป็น โอลิมปิกรอบแรก ก็ได้

อ้อ. เกือบลืมตอบคำถามของน้อง M@cpie ไปเลย.
ตำราที่เป็นภาษาไทย ที่พี่รู้จักและเคยเห็นมีอยู่แค่ 2 เล่มครับ.
1. ของ อ.มานัส เป็นอาจารย์ที่รามคำแหง มีวางขายที่ศูนย์หนังสือราม ฯ มี key ขายประกอบด้วย. ถ้าที่ศูนย์ไม่มี ก็ไปหาซื้อได้ที่ร้านหนังสือมือสอง ฝั่งตรงข้ามกับศูนย์หนังสือราม อยู่ในซอยซักซอยไม่ลึก 10 ก้าวก็ถึงแล้ว ถ้าหาไม่เจอลองถามเด็กรามแถวนั้นดู น่าจะรู้กันดี

ของใครอีกสักคน เพิ่งวางขายได้ราว 1 ปี อันนี้ไม่แนะนำครับ. เพราะเท่าที่ยืนเปิดอ่านผ่าน ๆ ร้อย 80 เหมือนกับของ อ.มานัส ซึ่งก็คงเป็นงั้น เพราะท้ายเล่มมีอ้างอิงของ อ.มานัส อยู่ด้วย

2. ตำราภาษาอังกฤษ มีที่แยกเป็นเล่มเดี่ยว ๆ ชื่อ ทำนองว่า Theory of eq... กับ include รวมในตำราประเภท Algebra ซึ่งเป็นเล่มแยกเดี่ยว ๆ พี่พอรู้ว่าอะไรดังแต่ไม่มีครับ เลยแนะนำไม่ได้ ส่วนที่ include รวมในตำรา Algebra มีอยู่อย่างน้อย 2 ที่ Highly recommend ครับ. คือ ห้องสมุดคณิตศาสตร์ กับ ห้องสมุดคณะวิศวะเราเอง (ตรงโซนหนังสือเก่าริมหน้าต่าง) มี key ด้วย โด่งดังเมื่อยุคปี 198x - 1900 ต้น ๆ มากครับ. ถ้าจำไม่ผิดของ Hall knights มั้งครับ. ตอนนี้พี่ก็กำลังตามล่าหาสุดยอดหนังสือ Algebra อีกเล่มหนึ่งอยู่ ไม่ขอบอกว่าเป็นของใครนะครับ. เพราะยังหาไม่ได้เลย

เนื้อหา Theory of eq โดยภาพรวมก็ตามชื่อล่ะครับ เกี่ยวข้องกับลูกเล่นทางสมการ เช่น การแก้สมการ 2,3,4 การลดรูปสมการจาก 5 หรือ มากกว่าลงมารูปง่ายขึ้น เช่น x⁵ + ax + b, x⁵ + ax⁴ + b, การประมาณช่วงของราก ค่าของราก โดยใช้ ทบ.ต่าง ๆ .... นี่เป็นขั้นต้น ถ้าสูงขึ้นไปก็จะมีพวก Algebraic function อะไรไปเรื่อยเปื่อย อย่างเรา ๆ ท่าน ๆ แค่ ทฤษฎีสมการเบื้องต้นก็น่าจะเพียงพอครับ.

อ่า ขอบคุณครับ ช่วงนี้คงไม่มีเวลาสนใจอย่างอื่นเลย
field ที่เรียน เน้นแต่พวก Calculus กับ applied math ไว้มีโอกาสจะแว่บๆไปดูครับ

สวัสดีครับ ไม่เห็นมีคนตอบกระทู้เริ่มต้นเลยนะครับ
cos p/5 * cos 2p/5 * cos 3p/5 * cos 4p/5
= cosp/5* cos 2p/5 * cos(p-2p/5) * cos(p-p/5)
= ( cosp/5* cos 2p/5 )2
= ( 2sinp/5*cosp/5* cos 2p/5 )2 /(2sinp/5)2
= (sin2p/5*cos2p/5)2 /(2sinp/5)2
= (sin4p/5)2 /16(sinp/5)2
=1/16

ส่วนของพี่กรนะครํบ ตอนนี้ทำได้แค่ข้อเดียวครับ
cos3 2p/13) + cos3 (4p/13) + cos3 (6p/13) + cos3 (8p/13) + cos3 (10p/13) + cos3 (12p/13)
= cos(2p/13) * cos2 (2p/13) +... (ทำแบบนี้ทุกตัวอ่ะนะครับ ขี้เกียจพิม)
= cos(2p/13) * (1+cos(4p/13)/2 + .....
= [cos(2p/13) + cos(2p/13) * cos(4p/13)]/2 +....
= [cos(2p/13) + (cos(6p/13) + cos(2p/13))/2 ]/2 +....
= [3cos(2p/13) + cos(6p/13]/4 + [3cos(4p/13) + cos(12p/13]/4 + ...
= 3[cos(2p/13) + cos(4p/13) + ... + cos(12p/13)]/4 + [cos(6p/13) + cos(12p/13) + ... + cos(36p/13)]/4
แล้วก้อใช้อนุกรมของ cos อ่ะคับ จะได้ -1/2 พี่กรใช้วิธีนี้ป่าวคับ
แล้วข้อสองพี่กรใบ้ให้ผมหน่อยได้ป่ะคับ คิดมา 2 วันละยังไม่ออกเลย