1. ถ้า $(x,y)\in R$ ที่ทำให้ $(x+5)^2+(y-12)^2=14^2$ จงหาค่าต่ำสุดของ $x^2+y^2$
[-SIL-]
ถ้าให้ $x^2+y^2=r^2$
จะได้ว่า $x^2+y^2$ มีค่าต่ำสุดเมื่อ $r = BO$ ตามรูปครับ
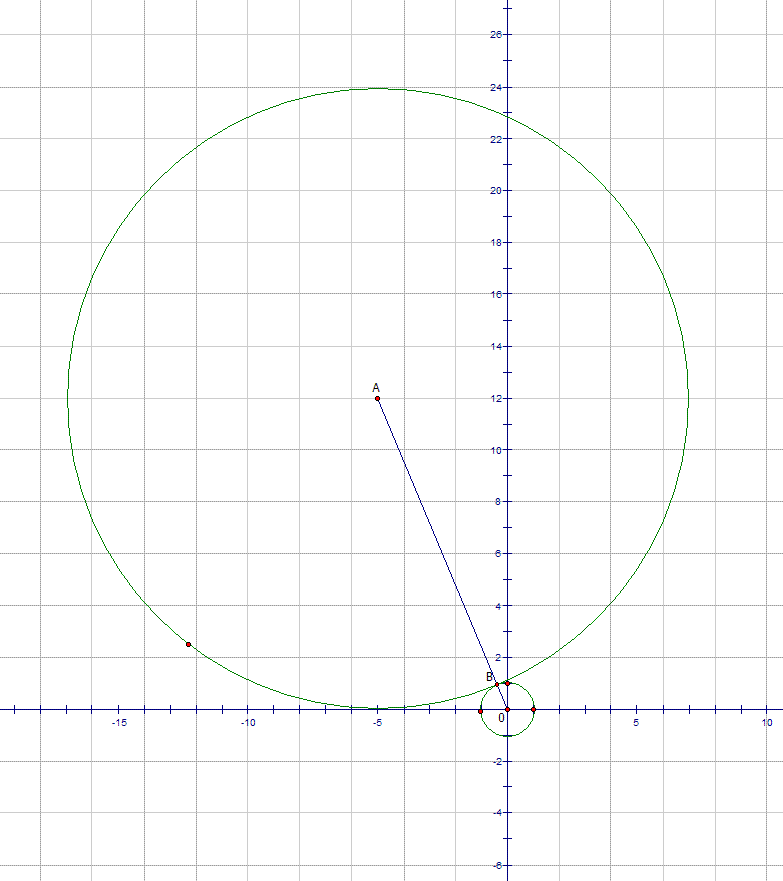
ดังนั้น $x^2+y^2 = (AO - AB)^2 = (13 -12)^2 = 1$
ถ้าต้องการหาจุด B ก็แก้สมการหาจุดตัดเอา
(รูปผมวาดผิดครับ วาดรัศมีเป็น 12)
ขอโทษคุณหยินหยางด้วยครับ ไม่ทันดูว่ามีหน้า 2 คุณหยินหยางวาดรูปไว้แล้ว หน้าแตกเลยครับ