
 |
|
|||||||
| สมัครสมาชิก | คู่มือการใช้ | รายชื่อสมาชิก | ปฏิทิน | ข้อความวันนี้ | ค้นหา |
  |
|
|
เครื่องมือของหัวข้อ | ค้นหาในหัวข้อนี้ |
|
#1
|
||||
|
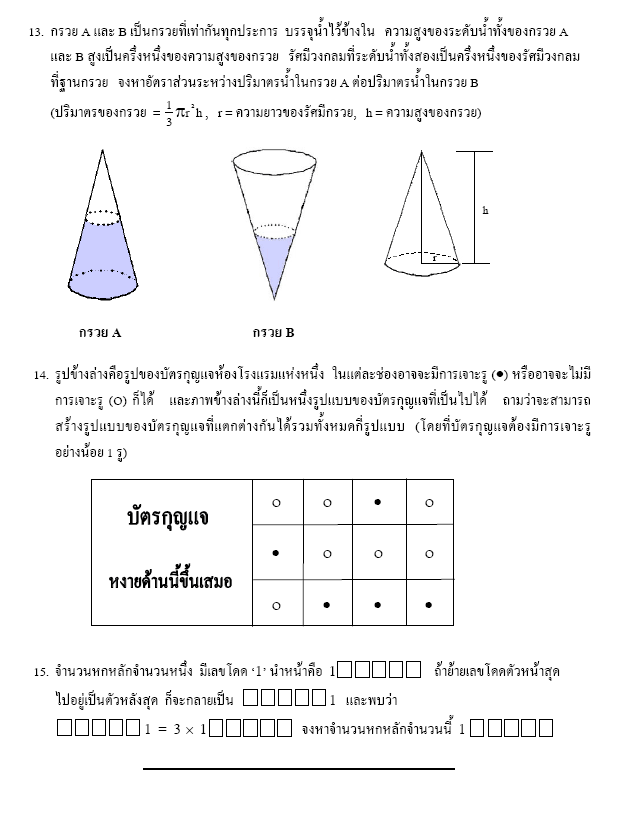
||||
|
board เงียบไปนาน ลองดู ข้อสอบระดับโลกที่ ฮ่องกงต่อนะครับ

__________________
เมื่อคิดจะทำอะไร หากคิดมากไป เมื่อไหร่จะได้ลงมือทำ 
|
|
#2
|
||||
|
||||
|
หน้า 2 ครับ

__________________
เมื่อคิดจะทำอะไร หากคิดมากไป เมื่อไหร่จะได้ลงมือทำ 
|
|
#3
|
||||
|
||||
|
ท้ายสุดแล้วครับ
__________________
เมื่อคิดจะทำอะไร หากคิดมากไป เมื่อไหร่จะได้ลงมือทำ 
|
|
#4
|
||||
|
||||
|
รอบแรก~~~~
1. ให้ x เป็นจำนวนดังกล่าว จะได้ x-4=a2, x+15=b2 (a,b เป็นจำนวนเต็ม) ดังนั้นจะได้ b2-a2=19 แก้สมการหาค่า a,b จะได้ x=85 2. เลือกจำนวนเฉพาะหนึ่งตัวจากสี่ตัว (2,3,5,7) หลักที่เหลือให้เป็น 1 ดังนั้นมีจำนวนสี่หลักที่สอดคล้องทั้งหมด 16 จำนวน 3. จากจุด O ลาก OX,OY ตั้งฉากกับ BC,CD ตามลำดับ ให้ OE ตัด BC ที่ M และให้ OG ตัด CD ที่ N และ จะพบว่าสามเหลี่ยม OXM และสามเหลี่ยม OYN เท่ากันทุกประการ ดังนั้นพื้นที่ส่วนที่แรเงาจึงเท่ากับพื้นที่สี่เหลี่ยมจัตุรัส OMCN หรือเท่ากับ 0.25 ตารางหน่วย 5. จำนวนนี้คือ 61 (โดย Chinese remainder theorem) 7. จำนวนที่สอดคล้องเงื่อนไขคือ 1993, 1981, ..., 1 ซึ่งมีทั้งหมด 167 จำนวน 9. ลาก PR จะได้ PR ขนานกับ AD ดังนั้นพื้นที่สี่เหลี่ยม PQRS= 0.5*16=8 ตารางเซนติเมตร 10. ให้ k เป็นเศษที่เท่ากัน จะได้จำนวนที่ต้องการเป็น ห.ร.ม. ของ 24-k, 56-k, 104-k นั่นคือ 16 13. ปริมาตรน้ำในกรวย A:ปริมาตรน้ำในกรวย B=\( \displaystyle\large{ \frac{1-\frac{1}{2}\cdot\frac{1}{4}}{\frac{1}{2}\cdot\frac{1}{4}} }=7:1\) 14. จำนวนกรณีทั้งหมด=2^12-1=4095 แบบ
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
|
#5
|
||||
|
||||
|
คุณ NongTum ทำตกข้อ 15 ไปหรือเปล่าครับ.
 สุดยอดมากทำได้เกือบหมดเลย เดี๋ยว My Maths เล่ม 8 นี้ว่าจะลงผลสอบของปีนี้ที่เด็กเราไปสอบมาเมื่อเดือน ก.ค. ครับ เห็นคุณ punk ซึ่งไปช่วยติวเด็กคนหนึ่งไปสอบบอกว่าข้อสอบปีนี้ มีเรื่องตรีโกณออกด้วย ไม่รู้ว่าจริงหรือเปล่า สุดยอดมากทำได้เกือบหมดเลย เดี๋ยว My Maths เล่ม 8 นี้ว่าจะลงผลสอบของปีนี้ที่เด็กเราไปสอบมาเมื่อเดือน ก.ค. ครับ เห็นคุณ punk ซึ่งไปช่วยติวเด็กคนหนึ่งไปสอบบอกว่าข้อสอบปีนี้ มีเรื่องตรีโกณออกด้วย ไม่รู้ว่าจริงหรือเปล่า ปล. ใครมีความสามารถหาข้อสอบของปีนี้มาได้ก็ดีนะครับ. ผมยังไม่ได้ลองหาดูเลยอยากเ็ห็นเหมือนกันว่ามีตรีโกณจริงหรือเปล่า  |
|
#6
|
||||
|
||||
|
รอบที่สอง~~~
4. ให้รถไฟขบวนแรกและขบวนที่สองวิ่งด้วยความเร็ว x และ y และมาพบกันหลังจากผ่านไป h ชั่วโมง โดยไม่เสียนัย ให้ระยะทางทั้งหมดยาว 1 ดังนั้นจะได้ 1=(h+3)x=(h+12)y=h(x+y) และจะได้ว่า 3x=hy, 12y=hx หรือ x:y=h:3=12:h หรือ h=6 นั่นคือ x:y=6:3=2:1 6. (ข้อนี้แนะนำให้วาดรูปประกอบ) ให้ด้านของหกเหลี่ยมเป็น 5,7,4,6,b,a ตามลำดับ แบ่งครึ่งมุมภายในระหว่างด้านที่ยาว 5 และ 7, 4 และ 6, 6 และ b, b และ a ต่อเส้นแบ่งครึ่งมุมไปตัดด้านตรงข้าม ให้ชื่อเส้นตรงเหล่านี้เป็น l1-l4 ตามลำดับ จากรูป(มีรูปแล้วนะครับ) a||l1||l3||4 และ b||l2||l4||7 โดยสมบัติของสี่เหลี่ยมด้านขนาน จะได้ว่า 7-(b-5)=6 และ 5-(6-a)=4 หรือ a+b=11 8. เราจะแจงกรณีดังนี้ ก) หลักแรกและหลักที่สี่เป็นศูนย์หรือหนึ่ง จะเลือกหลักที่สองและห้าได้หนึ่งตัวจาก 0-5 และหลักที่สามและหกได้หนึ่งตัวจาก 0-5 รวมทั้งสิ้น 2*6*6=72 จำนวน ข) หลักแรกและหลักที่สี่เป็นสอง จะเลือกหลักที่สองและห้าได้หนึ่งตัวจาก 0-3 และหลักที่สามและหกได้หนึ่งตัวจาก 0-5 รวมทั้งสิ้น 1*4*6=24 จำนวน รวมทั้งหมด 96 กรณี 11. ลาก AC, DB เนื่องจาก BB'=2BC, AB=BA' จะได้ว่า DA'BB'=2DABC ในทำนองเดียวกันจะได้ DB'CC'=2DBCD, DC'DD'=2DACD, DD'AA'=2DABD ดังนั้น พื้นที่สี่เหลี่ยม A'B'C'D'=1+2(DABC+DADC+DBCD+DABD)=1+2(1+1)=5 ตารางหน่วย 15. ให้จำนวนนี้คือ 1abcde เนื่องจาก 3*7=21 ดังนั้น e=7 จาก 1abcd7*3=abcd71 จะได้ d*3+2 ลงท้ายด้วย 7 หรือ d=5 (เพราะ 3*5=15) จาก 1abc57*3=abc571 จะได้ c*3+1 ลงท้ายด้วย 5 หรือ c=8 (เพราะ 3*8=24) จาก 1ab857*3=ab8571 จะได้ b*3+2 ลงท้ายด้วย 8 หรือ b=2 (เพราะ 3*2=6) จาก 1a2857*3=a28571 จะได้ a*3+0 ลงท้ายด้วย 2 หรือ a=4 (เพราะ 3*2=12) ดังนั้น จำนวนนี้คือ 142857 (หมายเหตุ: ลองสังเกตเลขทศนิยมของ 1/7 และ 3/7 ดูนะครับ) 12. (ไม่แน่ใจนะครับ เพราะเงื่อนไขที่ให้มากว้างเกินไป แต่ขอโพสต์ก่อน ใครคิดออกหรืออยากเสนออะไรเพิ่มเติม เชิญได้ครับ) จาก p+q+r=14 เมื่อ p,q,r แตกต่างกันทั้งหมด เราจะได้ (p,q,r,pqr) ที่เป็นไปได้ดังต่อไปนี้(ไม่นับ Permutation) (1,2,11,22), (1,3,10,30), (1,4,9,36), (1,5,8,40), (1,6,7,42), (2,3,9,54), (2,4,8,64), (2,5,7,70), (3,4,7,84), (3,5,6,90)
__________________
คนไทยร่วมใจอย่าใช้ภาษาวิบัติ ฝึกพิมพ์สัญลักษณ์สักนิด ชีวิต(คนตอบและคนถาม)จะง่ายขึ้นเยอะ (จริงๆนะ) Stay Hungry. Stay Foolish. |
|
#7
|
||||
|
||||
|
มาช่วยทำข้อ12ครับ (พึ่งผ่านมาเจอ ก็เลยลองนั่งทำ)
ผลบวกของจำนวนทั้งสามคือ 14 A พูดว่า “ฉันรู้ว่าจำนวนที่ครูบอก B และ C ต่างกัน" แสดงว่า เลขของ A ต้องเป็นเลขคี่แน่ๆ เพราะ ถ้าเป็นเลขคู่ ก็จะทำให้มีโอกาสที่ B กับ C จะมีเลขเหมือนกัน เช่น ถ้า A เป็นเลข 2 ก็มีโอกาสที่ B กับ C อาจจะเป็น 6 ทั้งคู่ การที่ A รู้ว่าตัวเองเป็นเลขคี่ (1 3 5 7 9 11) จึงทำให้มั่นใจว่า B กับ C ต่างกัน B พูดว่า “ฉันรู้ว่าจำนวนที่ครูบอกเราทุกคนต่างกันทั้งหมด" แสดงว่า B นอกจากจะเป็นเลขคี่(ดังที่อธิบายในกรณีของA)แล้ว B ต้องเป็นเลขคี่ที่ไม่น้อยกว่า 7 (7 9 11) เพราะ ถ้า B น้อยกว่า 7 เช่น เป็นเลข 5 มันไม่ได้การันตีว่า จะมี A หรือ C ที่จะเหมือนตนหรือไม่ (เช่น A=5 C=4) การที่ A รู้ว่าตัวเองเป็นเลขคี่ทีไม่น้อยกว่า 7 (7 9 11) จึงทำให้มั่นใจว่า -เลขของ A กับ C ต่างกันแน่ๆ -เลขของ A กับ C น้อยกว่าของตัวเองแน่ๆ (ถ้า B เป็น 7 ขึ้นไป A กับ C ซึ่งเป็นจำนวนเต็มบวกไม่มีทางเท่ากับ B พราะจะทำให้ผลบวกของสามตัวเลขเกิน 14) ดังนั้น B จึงกล้าพูดได้เต็มปากเต็มคำว่า “ฉันรู้ว่าจำนวนที่ครูบอกเราทุกคนต่างกันทั้งหมด" C พูดว่า “ตอนนี้ฉันรู้แล้วว่าจำนวนทั้งสามคืออะไรบ้าง" เมื่อ C ฟังทั้งสองแล้ว C วิเคราะห์ได้ดังนี้ เลขที่เป็นไปได้ของ A = 1 3 5 เลขที่เป็นไปได้ของ B = 7 9 11 ตอนนี้เลขที่เป็นไปได้ของ C ได้แก่ 2 4 6 8 10 12 ตัด 8 10 12 ทิ้งก่อนเลย เพราะ ไปบวกกัับของ B แล้วเกิน 14 ถ้า C เป็น 2 Cไม่สามารถมั่นใจได้ว่า เลขของ A กับ B เป็นอะไร เพราะ อาจเป็นกรณี A=1 B=11 หรือ A=5 B=7 ก็ได้ เช่นกัน ถ้า C เป็น 4 Cไม่สามารถมั่นใจได้ว่า เลขของ A กับ B เป็นอะไร เพราะ อาจเป็นกรณี A=1 B=9 หรือ A=3 B=7 ก็ได้ ฉะนั้น เลขของ C ต้องเป็น 6 เท่านั้น เพราะมีกรณีเดียวที่ A+B = 8 นั่นคือ A=1 B=7 คำตอบของข้อนี้คือ 1x7x6=42 22 ธันวาคม 2009 00:51 : ข้อความนี้ถูกแก้ไขแล้ว 4 ครั้ง, ครั้งล่าสุดโดยคุณ whatshix |
|
#8
|
||||
|
||||
|
มาร่วมเฉลยข้อแรก.....ใช้วิธีการสมมุติตัวแปรก่อน
ให้ตัวเลขที่ต้องการหาคือ $a$ จะได้สมการว่า $a-4 = x^2$ $a+15 = y^2$ เอาสมการมาลบกันโดยให้$y^2$เป็นตัวตั้ง $y^2- x^2 = 19$ $(y-x)(y+x) = 19$......เป็นการแยกผลต่างกำลังสอง จะสรุปว่า $y-x = 1$ และ $y+x=19$ เพราะ19เป็นจำนวนเฉพาะ ที่ให้$ y-x=1$ ด้วยเหตุผลดังกล่าว แก้สมการได้$y=10$ และ$x=9$ แทนค่าได้ $a=85$ |
|
#9
|
||||
|
||||
|
4.ให้รถขบวนแรกขับด้วยความเร็ว $u$ รถขบวนที่สองขับด้วยความเร็ว$v$
ให้เมืองทั้งสองห่างกัน $y$ และรถทั้งสองขบวนมาพบกันหลังจากขับมาแล้ว$t$ชั่วโมง รถทั้งสองมาพบกันที่ระยะทาง $x$จากเมืองA รถขบวนแรกขับมาได้ $x$จากเมืองA $x=u$x$t$ รถขบวนที่สองขับมาได้ระยะทาง$y-x$จากเมืองB จะได้ว่า $y-x=v$x$t$ เนื่องจากเวลาเท่ากัน จะได้ว่า$t=\frac{x}{u} =\frac{y-x}{v}$ ย้ายข้างจัดรูปได้เป็น$\frac{u}{v}=\frac{x}{y-x}$ โจทย์กำหนดต่อว่า รถขบวนแรกขับต่อไปอีก 3 ชั่วโมงถึงสถานีB(เหลือระยะทางอีก $y-x$) และรถขบวนที่สองขับต่อไปอีก 12 ชั่วโมงถึงสถานีA(เหลือระยะทางอีก$x$) จะได้ว่า $y-x = 3$x$u$ และ$x= 12$x$v$ หยิบค่าไปแทนใน$\frac{u}{v}=\frac{x}{y-x}$ จะได้ว่า $\frac{u}{v}=\frac{12v}{3u}$ จัดข้างใหม่ได้ว่า $\frac{u^2}{v^2}=\frac{12}{3}$ $(\frac{u}{v})^2=4$ ดังนั้น $\frac{u}{v}=2$ ตอบว่า อัตราส่วนความเร็วของรถขบวนที่หนึ่งต่อขบวนที่สองคือ 2:1 30 มกราคม 2010 17:59 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ กิตติ เหตุผล: พิมพ์ไม่ครบ |
|
#10
|
||||
|
||||
|
10.ตอบ 16
เขียนออกมาได้ว่า$24 = k$x$a+x$ $56=k$x$b+x$ $104=k$x$c+x$ $k$คือจำนวนที่โจทย์ถาม $x$คือเศษที่เหลือเท่ากัน ตามสูตรเดิมจับมาลบกันจะได้ว่า $32 =k(b-a) = 16$x$2$ $48 =k(c-b) = 16$x$3$ $80=k(c-a) = 16$x$5$ จะได้ว่า $k = 16$ 30 มกราคม 2010 22:30 : ข้อความนี้ถูกแก้ไขแล้ว 1 ครั้ง, ครั้งล่าสุดโดยคุณ กิตติ เหตุผล: พิมพ์ผิด |
|
#11
|
||||
|
||||
|
ขอทำข้อ12 อีกแบบนะครับ
จากที่ทราบว่า A รู้ว่าตัวเองเป็นจำนวนคี่มาแล้ว และ B มั่นใจว่าตัวเองรู้ว่า จำนวนทั้งสามมีค่าต่างกันหมด B น่าจะได้เลขคู่มาครับซึ่งก็ เป็นไป ได้ 2,4,6,8,10,12 ถ้า เป็น " 2 ", 2+12=14 ,คู่อันดับที่เป็นจำนวนคี่สองตัวบวกกันเป็น 12 มี (1,11),(3,9),(5,7) " 4 " , คู่อันดับที่เป็นจำนวนคี่สองตัวบวกกันเป็น 10 มี (1,9),(3,7),(5,5) " 6 " , คู่อันดับที่เป็นจำนวนคี่สองตัวบวกกันเป็น 8 มี (1,7),(3,5) " 8 " , คู่อันดับที่เป็นจำนวนคี่สองตัวบวกกันเป็น 6 มี (1,5),(3,3) " 10 " , คู่อันดับที่เป็นจำนวนคี่สองตัวบวกกันเป็น 4 มี (1,3) " 12 " , คู่อันดับที่เป็นจำนวนคี่สองตัวบวกกันเป็น มี (1,1) ดังนั้น เลขที่เป็นไปได้ที่ B ได้มาก็คือ 2,6,10 จาก C บอกว่ารู้ละว่ามีเลขอะไรมั่ง ดังนั้น C ต้องได้เลข 11 มาแหงๆครับ 1+2+11=14 ดังนั้นข้อนี้ตอบ 22 ตรวจให้ผมทีนะครับ 
__________________
I'm kak. |
  |
|
|